Hello Aspirants
We have come up with Sectional Tests for upcoming LIC AAO 2019 Prelim Exam. Practice the questions to ace the exam.
Directions(1-4): Compare both the equations and choose a correct option.
- I.6x^2 – 25x + 14 = 0
II.2y^2 – 13y + 6 = 0x>=yx > yy>=xy > xNo relationOption E
I.6x^2 – 25x + 14 = 0
=>6x^2 -21x – 4x + 14 = 0
=>(2x-7)(3x – 2) = 0
=> x = 7/2, 2/3
II.2y^2 – 13y + 6 = 0
=>2y^2 – 12y – y + 6 = 0
=>(y-6)(2y – 1) = 0
=> y = 6, ½
No relation. - I.5x^2 – 27x + 10 = 0
II.y^2 – 14y + 48 = 0
y > xNo relationy>=xx > yx>=yOption A
I.5x^2 – 27x + 10 = 0
=>5x^2 – 25x – 2x + 10 = 0
=>(x-5)(5x-2) = 0
=>x = 5,2/5
II.y^2 – 14y + 48 = 0
=>y^2 – 8y – 6y + 48 = 0
=>(y-8)(y-6) = 0
=> y = 8,6
y > x - I.x^2 + 12x + 32 = 0
II.y^2 + 10y + 16 = 0
x > yy>=xNo relationx>=yy > xOption C
I.x^2 + 12x + 32 = 0
=>x^2 + 8x + 4x + 32 = 0
=>(x+4)(x+8) = 0
=>x = -4,-8
II.y^2 + 10y + 16 = 0
=>y^2 + 2y + 8 y + 16 = 0
=>(y+2)(y+8) = 0
=> y = -2,-8
No relation. - I.2x^2 – 18x + 36 = 0
II.2y^2 – 30y + 108 = 0
No relationx > yy > xy>=xx>=yOption D
I.2x^2 – 18x + 36 = 0
=>2x^2 – 12x – 6x + 36 = 0
=>(2x-6)(x – 6) = 0
=> x = 3,6
II.2y^2 – 30y + 108 = 0
=>2y^2 – 12y – 18u + 108 = 0
=>(2y – 18)(y-6) = 0
=> y = 6,9
y>=x - 750 *(10.24)^1/2 = ?% of 480
500440320400510Option A
750 *(10.24)^1/2 = ?% of 480
=>750*3.2 = ?*4.8
=>? = 500 - (75% of 1820) – 25^2 = ?^2 -25% of 176
2018112817Option D
75% of 1820) – 25^2 = ?^2 -25% of 176
=>?^2 – ¼*176 = 0.75*1820 – 625
=>?^2 – 44 = 1365- 625
=>?^2 = 740 + 44
=>? = 28 - {(484)^1/2 + 224 / 2^3 }% of 960 = ?% of 640
6681707590Option D
{(484)^1/2 + 224 / 2^3 }% of 960 = ?% of 640
=>?% of 640 = (22+28)% of 960
=>? * 6.4 = 480
=>? = 75 - (600/24)*25 + 25^2 + 125% of 280 = ?^2
3340254153Option B
(600/24)*25 + 25^2 + 125% of 280 = ?^2
=>?^ 2 = 25*25 +625 + 350
=>?^2 = 1250 + 350
=> ? = 40 - 15*8 + ? – 9 * 11 = 12*18
195152170164175Option A
15*8 + ? – 9 * 11 = 12*18
=> 120 + ? – 99 = 216
=>? + 21 = 216
=>? = 195 - 16% of 1750 -20% of 1150 =25% of ?
110100200324220Option C
16% of 1750 -20% of 1150 =25% of ?
=>0.25*? = 0.16*1750 – 0.20*1150
=>0.25*? = 280 – 230
=>? = 200 - 244 – 156 + ?^2 -13^2 = 15*14 + 25*22
2016142919Option D
244 – 156 + ?^2 -13^2 = 15*14 + 25*22
=>88 + ?^2 – 169 = 210 + 550
=>?^2 – 81 = 760
=>?^2 = 841
=> ? = 29 - {(3072/16)/8)/4}+ 14^2 = ?
195174166202188Option D
{(3072/16)/8)/4}+ 14^2 = ?
=>? = {(192/8)/4} + 14^2
=> ? = 24/4 +196
=>? = 202 - 648/9 + 18^2 – 20% of 630 = ?*6
4122303545Option E
648/9 + 18^2 – 20% of 630 = ?*6
=>?*6 = 72 + 324 – 0.20*630
=>?*6 = 396 – 126
=>?*6 = 270
=> ? = 45 - 613 + 762 + ? – 981 = 549 – 375 + 817
660597500495510Option B
613 + 762 + ? – 981 = 549 – 375 + 817
=>1375 + ? – 981 = 991
=>394 + ? = 991
=>? = 597 - 84^2 – 79^2 + (1936)^1/2 – 20% of 980 = ?
740600548663875Option D
84^2 – 79^2 + (1936)^1/2 – 20% of 980 = ?
=>815 + 44 – 196 = ?
=>? = 663 - 958, 833, 733, 658, 608, (?)
448415583574545Option C
958, 833, 733, 658, 608, (?)
958 – 833 = 125
833 – 733 = 100
733 – 658 = 75
658 – 608 = 50
? = 608 – 25 = 583 - 11, 10, 18, 51, 200, (?)
900880995745717Option C
11 × 1 – 1 = 10
10 × 2 – 2 = 18
18 × 3 – 3 = 51
51 × 4 – 4 = 200
200 × 5 – 5 = 995 - 25, 48, 94, 186, 370, (?)
695687770712738Option E
25 × 2 – 2 = 50 – 2 = 48
48 × 2 – 2 = 96 – 2 = 94
94 × 2 – 2 = 188 – 2 = 186
186 × 2 – 2 = 372 – 2 = 370
370 × 2 – 2 = 740 – 2 = 738 - 14, 24, 43, 71, 108, (?)
154140125136118Option A
14 + 10 = 24
24 + 19 (=10 + 9) = 43
43 + 28 (= 19 + 9) = 71
71 + 37 (= 28 + 9) = 108
108 + 46 (=37 + 9) = 154 - 144, 173, 140, 169, 136, (?)
140165157125133Option B
144 + 29 = 173
173 – 33 = 140
140 + 29 = 169
169 – 33 = 136
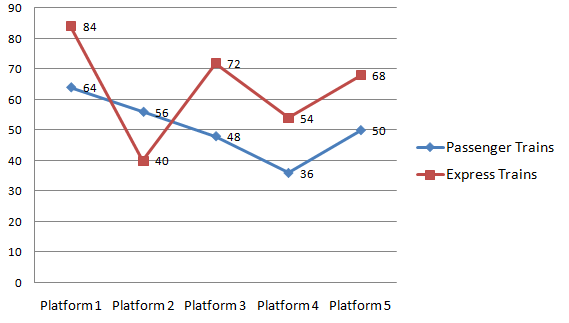
136 + 29 = 165 - The respective ratio of number of Passenger trains to the number of Express trains passing through platform number 7 is 5:7. If the total number of trains passing through platform number 7 is 50% more than the total number of trains passing through platform number 2. Find the number of Passenger trains passing through platform number 7.
7152456084Option D
Total number of trains passing through platform number 2 = 56+40 = 96
Total number of trains passing through platform number 7 = 96*1.5 = 144
Total number of Passenger trains passing through platform number 7 = 5/12*144 = 60 - The number of passenger trains passing through platform number 6 to the number of passenger trains passing through platform number 5 are in the ratio 4:5 resp. and the number of Express trains passing through platform number 6 are 25% more than number of Express trains passing through platform number 5 . Find the total number of trains passing through platform number 6.
125111108114117Option A
Total number of Passenger trains passing through platform number 6 = 50/5*4 = 40
Total number of Express trains passing through platform number 6 = 68*1.25 = 85
Total number of trains passing through platform number 6 = 40+85 = 125 - Find the ratio of number of trains passing through platform number 2 to the total number of trains passing through platform number 3?
1:33:24:55:73:4Option C
Total number of trains passing through platform number 2 = 56+40 = 96
Total number of trains passing through platform number 3 = 48+72 = 120
Required ratio = 4:5 - Total number of trains passing through platform number 4 is what percentage more or less than the number of Express trains passing through platform number 3?
32%10%18%25%20%Option D
Total number of trains passing through platform number 4 = 36+54 = 90
Required% = (90-72)/72*100 = 25% - Find the average of the number of passenger trains passing through platform number 1,2 and 3 taken together.
3038445647Option D
Required average = (64+56+48)/3 = 56 - Prakash borrowed some money at the rate of 3 percent per annum for the first 4 years, 7 percent per annum for the next 5 years and at the rate of 9 percent per annum for the next 7 years. If the total interest paid by him at the end of 16 years is 4400. Find the money borrowed by Prakash?
Rs.3000Rs.2000Rs.4000Rs.6000Rs.5000Option C
Let the sum be Rs.x.
(3*4*x)/100 + (7*5*x)/100 + (9*7*x)/100 = 4400
=>x = 440000/110 = Rs.4000 - Prabir invests an amount of Rs.15860 in the names of her three daughters A,B and C in such a way that they get the same interest after 2,3 and 4 years resp. If the rate of interest is 5% p.a. Find the ratio of the amounts invested among A,B and C.
1:4:25:3:73:7:25:1:46:4:3Option E
(P1*2*5)/100 : (P2*3*5)/100 : (P3*4*5)/100
=> 10P1 : 15P2 : 20P3
=>P1:P2:P3 =30:20:15 = 6:4:3 - If numerical value of percentage markup price, marked price per kg and percentage discount offered on marked price of a product are in the ratio 20:12:9. Find the percentage profit on the product.
7.7%9.2%5.8%6.5%8.3%Option B
MP = 12
SP = (100-9)/100*12 = 10.92
Let CP be x.
(100+20)/100*x = 12
=> x= 10
Profit% = 0.92/10*100 = 9.2% - Sahil buys wheat at Rs.10 per kg and puts a price tag on it so as to earn a profit of 30%. However his faculty shows 1 kg when it is actually 700 gm. What is his actual profit percent?
613/2%600/7%515/4%623/8%551/5%Option B
CP of 1 kg = Rs.10
CP of 1 gm = 1/100
SP of 700 gm = Rs.13
SP of 1 gm = 13/700
Profit% = {[13/700 – 1/100]/[1/100]}*100 = 600/7% - To do a certain work A is 100/3% more efficient than B. They started to work alternatively on the same work starting from A on one day and B on day two and finished 60% of work in 30 days. Find the time taken by A alone to finish the whole work?
163/5 days157/2 days166/5 days175/4 days171/3 daysOption D
Ratio of efficiency of A and B is 4:3.
Let in one day A does 4x unit of work and in one day B does 3x unit of work.
In 30 days 60% work is completed.
So, in 50 days whole work will be completed.
In 2 days 7x unit is completed so in 50 days.
= 50*7x/2 unit done
Whole work is completed by A in = (50*7x)/(4x*2) = 175/4 days - A car covered 48 km less in T hours than a train, if speed of train is 25% more than the speed of car, which is 64 km/hr. and speed of an aircraft is 62(1/2)% more than the sum of speed of car and train. Find how much distance will be covered by aircraft in (T-1/4) hour?
873.7 km741.6 km555.5 km643.5 km612.4 kmOption D
Speed of train = 64*5/4
= 80 km/hr.
Now,
80T – 64T = 48
=>T = 3 hours
Speed of Aircraft = (144*13/8) = 234 km/hr.
Required distance = 234*(3 – 1/4) = 643.5 km - Sam invested some amount in scheme P which offers 20% C.I. p.a. while some amount in scheme Q which offers 8% S.I. p.a. After 2 years, ratio of interest earn from P to Q is 11:6. Amount invested by Sam in scheme P is what percent of the amount invested by him in scheme Q.
53(4/5)%66(2/3)%44(2/7)%50(1/2)%61(3/5)%Option B
Let the amount invested in scheme P and Q be x and y resp.
x*[(120/100)^2 – 1]/(y*8*2/100) = 11/6
=>(x*0.44)/(y*0.16) = 11/6
=>x / y = 2/3
Required% = 2/3*100 = 66(2/3)% - There are two vessels A and B which contains mixture of sulphuric acid and nitrous oxide in the ratio of 7:2 and 3:4 resp. Mixture of both vessels are mixed to obtain a mixture of 390 ml, in which quantity of nitrous oxide is 160 ml. Find the ratio of quantity of mixture in vessel A to quantity of mixture in vessel B ?
3:42:56:77:83:5Option C
Let the total mixture of sulphuric acid and nitorus oxide in vessel A and vessel B be x and y resp.
x + y = 390 – (1)
2x/9 + 4y/7 = 160
14x+36y = 10080 –(2)
On solving these two equations, we get
x = 180 ml
y = 210 ml
Required ratio = 6:7 - The surface of sphere is 423.5 cm^2 less than total surface area of a hemisphere. If ratio between radius of hemisphere and sphere is 3:2. Find the radius of hemisphere?
8.4 cm12.3 cm13.7 cm7.4 cm10.5 cmOption E
3*pi*r*r*r – 4*pi*r*r = 423.5
=>x = 3.5 cm
Radius of hemisphere = 21/2 = 10.5 cm - In first bucket there are five apples, Y oranges and 7 bananas. Probability of drawing one orange from bucket is 2/5. In second bucket there are (Y-3) apples, (Y-4) oranges and 6 bananas, if two fruits are drawn from second bucket. Find the probability that both are apples?
1/174/272/214/233/19Option C
Probability of drawing one orange = Y/(12+Y) = 2/5
=> Y = 8
Required Probability = 5C2/15C2 = 2/21
Directions(5-20): What will be the approximate value come in place of question mark ‘?’ in the following questions.
Directions(21-25): Answer the following questions based on the following graph.
The given chart shows the number of Passenger trains and Express trains passing through different platforms of a railway station on a particular day.

What?s Happening i am new to this, I stumbled upon this I’ve found It positively useful and it has helped me out loads. I hope to contribute & assist other users like its aided me. Great job.
I have learned new things through the blog post. Also a thing to I have observed is that generally, FSBO sellers will certainly reject people. Remember, they might prefer to not use your services. But if a person maintain a gradual, professional relationship, offering assistance and being in contact for four to five weeks, you will usually be able to win interviews. From there, a house listing follows. Many thanks
Thanks for your submission. I also believe that laptop computers are becoming more and more popular nowadays, and now are sometimes the only form of computer found in a household. Simply because at the same time they are becoming more and more very affordable, their working power is growing to the point where they’re as highly effective as personal computers from just a few years ago.
Good article. It is rather unfortunate that over the last decade, the travel industry has already been able to to handle terrorism, SARS, tsunamis, bird flu virus, swine flu, plus the first ever true global tough economy. Through it all the industry has proven to be powerful, resilient in addition to dynamic, finding new ways to deal with difficulty. There are always fresh troubles and the possiblility to which the sector must all over again adapt and act in response.
Hi there, I found your blog via Google while searching for a related topic, your site came up, it looks good. I have bookmarked it in my google bookmarks.
Great post. I was checking constantly this blog and I am impressed! Very helpful info specially the last part 🙂 I care for such information much. I was seeking this particular info for a very long time. Thank you and good luck.
A powerful share, I just given this onto a colleague who was doing just a little analysis on this. And he actually purchased me breakfast as a result of I discovered it for him.. smile. So let me reword that: Thnx for the treat! But yeah Thnkx for spending the time to discuss this, I really feel strongly about it and love studying extra on this topic. If attainable, as you turn into experience, would you thoughts updating your weblog with extra details? It’s highly helpful for me. Large thumb up for this weblog publish!
Thanks for some other wonderful article. Where else could anybody get that kind of info in such a perfect approach of writing? I have a presentation subsequent week, and I’m on the look for such information.
I?m now not certain where you are getting your information, however great topic. I must spend a while studying much more or figuring out more. Thank you for wonderful info I used to be looking for this info for my mission. Aussie John’s Ducted Gas Heating Repairs and Installation 706 Bourke St, Docklands VIC 3008
Whats up! I simply wish to give a huge thumbs up for the great information you may have here on this post. I will likely be coming back to your weblog for extra soon.
I have observed that car insurance corporations know the autos which are prone to accidents along with risks. Additionally they know what sort of cars are given to higher risk as well as the higher risk they may have the higher the particular premium rate. Understanding the straightforward basics with car insurance just might help you choose the right form of insurance policy which will take care of your needs in case you happen to be involved in any accident. Thanks for sharing the ideas on your own blog.
It?s really a great and helpful piece of information. I?m glad that you shared this helpful info with us. Please keep us up to date like this. Thanks for sharing.
We are a group of volunteers and starting a new scheme in our community. Your website offered us with valuable info to work on. You’ve done a formidable job and our whole community will be thankful to you.
Would you be fascinated by exchanging hyperlinks?
One more thing to say is that an online business administration training is designed for students to be able to without problems proceed to bachelor degree education. The 90 credit diploma meets the other bachelor college degree requirements and once you earn the associate of arts in BA online, you will have access to the most recent technologies with this field. Some reasons why students want to be able to get their associate degree in business is because they’re interested in the field and want to obtain the general education and learning necessary previous to jumping into a bachelor diploma program. Thx for the tips you actually provide inside your blog.
Thank you for some other informative site. Where else may I get that type of info written in such an ideal approach? I have a mission that I’m simply now working on, and I have been on the glance out for such info.
Hi there! I simply want to give a huge thumbs up for the good information you might have right here on this post. I can be coming again to your weblog for more soon.
Hello there, You have done a great job. I will definitely digg it and personally recommend to my friends. I am confident they will be benefited from this web site.
Thanks for giving your ideas on this blog. As well, a myth regarding the lenders intentions any time talking about foreclosure is that the bank will not getreceive my payments. There is a fair bit of time that this bank will take payments in some places. If you are too deep in the hole, they may commonly call that you pay the payment 100 . However, that doesn’t mean that they will not take any sort of payments at all. In case you and the bank can seem to work anything out, the particular foreclosure approach may end. However, if you ever continue to miss out on payments beneath new approach, the foreclosed process can just pick up from where it left off.
You can certainly see your skills in the paintings you write. The world hopes for more passionate writers like you who aren’t afraid to mention how they believe. All the time follow your heart.
An fascinating dialogue is worth comment. I think that it is best to write more on this subject, it might not be a taboo subject but usually individuals are not sufficient to speak on such topics. To the next. Cheers
I do agree with all of the ideas you’ve presented in your post. They are very convincing and will definitely work. Still, the posts are too short for beginners. Could you please extend them a bit from next time? Thanks for the post.
Wow, awesome weblog structure! How lengthy have you ever been running a blog for? you make blogging glance easy. The full glance of your site is excellent, as neatly as the content!
Hey very cool web site!! Man .. Excellent .. Amazing .. I will bookmark your website and take the feeds also?I’m happy to find so many useful information here in the post, we need work out more strategies in this regard, thanks for sharing. . . . . .
hey there and thank you for your info ? I?ve definitely picked up anything new from right here. I did however expertise some technical points using this site, as I experienced to reload the website lots of times previous to I could get it to load correctly. I had been wondering if your web host is OK? Not that I’m complaining, but slow loading instances times will sometimes affect your placement in google and could damage your quality score if advertising and marketing with Adwords. Anyway I?m adding this RSS to my email and can look out for much more of your respective exciting content. Make sure you update this again very soon..
It?s actually a cool and helpful piece of information. I am glad that you shared this helpful info with us. Please stay us up to date like this. Thank you for sharing.
Heya i?m for the primary time here. I found this board and I to find It really useful & it helped me out a lot. I am hoping to provide something again and help others such as you helped me.
Normally I don’t learn post on blogs, however I would like to say that this write-up very compelled me to check out and do so! Your writing style has been surprised me. Thanks, very nice article.
I have recently started a blog, the information you offer on this website has helped me tremendously. Thanks for all of your time & work.
When I initially commented I clicked the -Notify me when new comments are added- checkbox and now every time a remark is added I get 4 emails with the identical comment. Is there any manner you may take away me from that service? Thanks!
Thanks for the various tips contributed on this site. I have noticed that many insurance firms offer customers generous savings if they elect to insure multiple cars with them. A significant quantity of households currently have several cars these days, specifically those with elderly teenage kids still living at home, and also the savings with policies can certainly soon mount up. So it will pay to look for a great deal.
I?m impressed, I need to say. Really not often do I encounter a weblog that?s both educative and entertaining, and let me let you know, you will have hit the nail on the head. Your concept is excellent; the difficulty is something that not sufficient individuals are speaking intelligently about. I’m very happy that I stumbled throughout this in my search for something referring to this.
I just could not go away your website prior to suggesting that I actually loved the standard info an individual provide in your visitors? Is going to be again regularly in order to check out new posts
Thanks for your article. I would like to say that the health insurance dealer also works for the benefit of the particular coordinators of any group insurance cover. The health insurance professional is given a summary of benefits wanted by a person or a group coordinator. What any broker will is hunt for individuals as well as coordinators which usually best match those wants. Then he gifts his recommendations and if both parties agree, the particular broker formulates legal contract between the 2 parties.
Love your blog! If you are ever in Nebraska, check out Omaha’s best chef-driven catering & party rooms in the metro area for over 25 years. Restaurants Inc. is known for its delicious American, Italian & Southwest Mexican dishes and as a locally and family-owned business, we understand the importance of having meticulous detail with whatever event you’re planning.
It?s really a nice and helpful piece of information. I am glad that you shared this useful information with us. Please keep us up to date like this. Thanks for sharing.
I don?t even know how I ended up here, but I thought this post was great. I do not know who you are but definitely you’re going to a famous blogger if you aren’t already 😉 Cheers!
I’ve learned a number of important things by means of your post. I would also like to mention that there is a situation where you will get a loan and don’t need a cosigner such as a Federal government Student Aid Loan. But when you are getting credit through a common loan service then you need to be prepared to have a cosigner ready to allow you to. The lenders will certainly base that decision on a few factors but the main one will be your credit rating. There are some loan merchants that will furthermore look at your work history and make up your mind based on that but in many cases it will hinge on your report.
Something more important is that while looking for a good online electronics retail outlet, look for online shops that are continuously updated, keeping up-to-date with the most up-to-date products, the top deals, as well as helpful information on product or service. This will ensure you are doing business with a shop that stays over the competition and provides you what you ought to make educated, well-informed electronics buying. Thanks for the crucial tips I have really learned through your blog.
Thanks for the points you have shared here. Yet another thing I would like to say is that personal computer memory demands generally increase along with other breakthroughs in the technology. For instance, any time new generations of processors are brought to the market, there is usually a corresponding increase in the size demands of both computer system memory as well as hard drive space. This is because the software operated by these cpus will inevitably surge in power to make new technological know-how.
Appreciate you for sharing these kind of wonderful content. In addition, an excellent travel in addition to medical insurance plan can often relieve those fears that come with journeying abroad. Some sort of medical crisis can rapidly become extremely expensive and that’s certain to quickly set a financial weight on the family’s finances. Putting in place the suitable travel insurance offer prior to leaving is worth the time and effort. Thanks a lot
I have really noticed that credit improvement activity ought to be conducted with tactics. If not, you will probably find yourself endangering your rating. In order to be successful in fixing your credit history you have to ascertain that from this time you pay your complete monthly expenses promptly in advance of their planned date. It is definitely significant simply because by certainly not accomplishing that area, all other steps that you will choose to adopt to improve your credit rank will not be successful. Thanks for giving your thoughts.
I?m impressed, I need to say. Actually not often do I encounter a blog that?s both educative and entertaining, and let me inform you, you will have hit the nail on the head. Your idea is excellent; the issue is one thing that not enough individuals are talking intelligently about. I am very completely happy that I stumbled throughout this in my seek for something regarding this.
Great work! This is the type of info that should be shared around the web. Shame on Google for not positioning this post higher! Come on over and visit my site . Thanks =)
Today, considering the fast life style that everyone leads, credit cards have a big demand throughout the market. Persons from every arena are using the credit card and people who not using the credit card have made arrangements to apply for just one. Thanks for expressing your ideas in credit cards.
I like the helpful information you provide in your articles. I?ll bookmark your blog and check again here frequently. I’m quite sure I will learn plenty of new stuff right here! Good luck for the next!
wonderful points altogether, you simply received a logo new reader. What may you suggest about your put up that you simply made a few days ago? Any sure?
You can definitely see your skills in the work you write. The world hopes for more passionate writers like you who are not afraid to say how they believe. Always follow your heart.
you are really a good webmaster. The site loading speed is amazing. It seems that you’re doing any unique trick. Also, The contents are masterwork. you’ve done a magnificent job on this topic!
I loved as much as you will receive carried out right here. The sketch is tasteful, your authored subject matter stylish. nonetheless, you command get bought an edginess over that you wish be delivering the following. unwell unquestionably come further formerly again since exactly the same nearly very often inside case you shield this increase.
Thanks for your post. I have generally observed that many people are needing to lose weight when they wish to show up slim as well as attractive. Having said that, they do not always realize that there are more benefits just for losing weight as well. Doctors say that fat people are afflicted with a variety of health conditions that can be directly attributed to their own excess weight. The good thing is that people who’re overweight along with suffering from numerous diseases are able to reduce the severity of their own illnesses by losing weight. It’s possible to see a slow but marked improvement in health as soon as even a small amount of fat reduction is realized.
Thanks for these guidelines. One thing I also believe is credit cards presenting a 0 apr often bait consumers together with zero interest rate, instant authorization and easy internet balance transfers, but beware of the real factor that is going to void your current 0 easy road annual percentage rate and also throw anybody out into the terrible house fast.
Thanks for the distinct tips discussed on this website. I have observed that many insurance providers offer customers generous special discounts if they opt to insure more and more cars with them. A significant amount of households have got several motor vehicles these days, particularly those with mature teenage children still located at home, and also the savings for policies can easily soon mount up. So it is a good idea to look for a bargain.
Thanks for expressing your ideas right here. The other issue is that if a problem comes up with a computer system motherboard, individuals should not consider the risk connected with repairing that themselves because if it is not done properly it can lead to irreparable damage to the complete laptop. In most cases, it is safe just to approach the dealer of your laptop for your repair of that motherboard. They will have technicians that have an know-how in dealing with pc motherboard complications and can have the right analysis and undertake repairs.
Thank you for the sensible critique. Me and my neighbor were just preparing to do a little research on this. We got a grab a book from our area library but I think I learned more clear from this post. I am very glad to see such excellent info being shared freely out there.
Yet another issue is that video games can be serious anyway with the key focus on mastering rather than amusement. Although, it comes with an entertainment factor to keep your children engaged, just about every game is often designed to develop a specific skill set or programs, such as math concepts or scientific discipline. Thanks for your article.
whoah this blog is great i love studying your posts. Stay up the great paintings! You already know, a lot of people are looking around for this information, you could aid them greatly.
There are some fascinating time limits in this article however I don?t know if I see all of them center to heart. There may be some validity however I’ll take maintain opinion until I look into it further. Good article , thanks and we wish more! Added to FeedBurner as effectively
Something else is that when looking for a good on the web electronics retail outlet, look for web stores that are continually updated, trying to keep up-to-date with the most up-to-date products, the perfect deals, and also helpful information on services and products. This will ensure you are getting through a shop that stays atop the competition and gives you things to make knowledgeable, well-informed electronics acquisitions. Thanks for the important tips I have really learned from your blog.
I do enjoy the manner in which you have presented this specific matter and it does give me some fodder for thought. However, from just what I have experienced, I only wish when other remarks pack on that men and women continue to be on issue and not start on a soap box regarding some other news du jour. Yet, thank you for this superb point and whilst I can not necessarily agree with it in totality, I respect the standpoint.
Thank you for the auspicious writeup. It in truth was a leisure account it. Look advanced to far brought agreeable from you! By the way, how can we keep up a correspondence?
I used to be very happy to seek out this web-site.I needed to thanks in your time for this wonderful learn!! I definitely enjoying each little bit of it and I’ve you bookmarked to take a look at new stuff you weblog post.
I have figured out some new points from your web site about pc’s. Another thing I have always assumed is that computers have become a product that each residence must have for many people reasons. They offer convenient ways in which to organize the home, pay bills, go shopping, study, focus on music and in some cases watch tv programs. An innovative solution to complete these types of tasks is by using a laptop computer. These computers are mobile, small, highly effective and transportable.
Thank you for sharing excellent informations. Your site is so cool. I am impressed by the details that you?ve on this site. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for more articles. You, my pal, ROCK! I found just the information I already searched all over the place and simply could not come across. What a great web-site.
Thanks for expressing your ideas. I would also like to mention that video games have been at any time evolving. Today’s technology and inventions have made it simpler to create practical and enjoyable games. These types of entertainment video games were not that sensible when the real concept was first being tried out. Just like other designs of technology, video games also have had to advance through many years. This itself is testimony for the fast development of video games.
With everything which appears to be building throughout this particular subject matter, a significant percentage of viewpoints are rather radical. Nevertheless, I beg your pardon, because I can not subscribe to your entire strategy, all be it stimulating none the less. It looks to me that your opinions are not entirely justified and in actuality you are generally yourself not entirely confident of your assertion. In any event I did enjoy reading it.
I was just searching for this info for some time. After six hours of continuous Googleing, at last I got it in your website. I wonder what is the lack of Google strategy that do not rank this kind of informative websites in top of the list. Generally the top sites are full of garbage.
In line with my observation, after a foreclosed home is available at a bidding, it is common for any borrower in order to still have some sort ofthat remaining balance on the mortgage loan. There are many lenders who make an effort to have all charges and liens paid off by the subsequent buyer. Nevertheless, depending on specific programs, legislation, and state regulations there may be many loans which are not easily sorted out through the switch of lending options. Therefore, the duty still remains on the consumer that has acquired his or her property in foreclosure process. Thanks for sharing your ideas on this website.
The following time I read a blog, I hope that it doesnt disappoint me as a lot as this one. I imply, I know it was my option to learn, but I truly thought youd have something interesting to say. All I hear is a bunch of whining about something that you possibly can repair should you werent too busy looking for attention.
Thanks for your blog post. I would like to say a health insurance specialist also works best for the benefit of the coordinators of any group insurance plan. The health insurance broker is given a directory of benefits searched for by anyone or a group coordinator. What a broker may is try to find individuals or even coordinators which best match those needs. Then he provides his recommendations and if all sides agree, the particular broker formulates a legal contract between the 2 parties.
Pretty portion of content. I just stumbled upon your web site and in accession capital to assert that I acquire actually loved account your weblog posts. Anyway I?ll be subscribing to your feeds and even I success you access persistently rapidly.
I just couldn’t leave your web site before suggesting that I extremely enjoyed the standard info an individual provide for your guests? Is going to be back regularly to inspect new posts
I do consider all the ideas you’ve presented to your post. They are really convincing and will definitely work. Nonetheless, the posts are too brief for newbies. May just you please prolong them a little from subsequent time? Thanks for the post.
Also I believe that mesothelioma cancer is a extraordinary form of cancer that is often found in individuals previously subjected to asbestos. Cancerous tissue form from the mesothelium, which is a protective lining which covers most of the body’s body organs. These cells usually form from the lining of the lungs, belly, or the sac which encircles the heart. Thanks for sharing your ideas.
I just could not depart your website before suggesting that I extremely enjoyed the standard information a person provide for your visitors? Is gonna be back often in order to check up on new posts
What?s Happening i am new to this, I stumbled upon this I’ve discovered It positively useful and it has aided me out loads. I hope to contribute & aid other customers like its helped me. Good job.
Thank you for the auspicious writeup. It in reality used to be a amusement account it. Glance complicated to more brought agreeable from you! However, how can we be in contact?
Thanks for this excellent article. One other thing is that most digital cameras can come equipped with a new zoom lens that permits more or less of a scene to become included through ‘zooming’ in and out. All these changes in {focus|focusing|concentration|target|the a**** length tend to be reflected in the viewfinder and on massive display screen right on the back of the particular camera.
okmark your blog and check again here frequently. I’m quite certain I will learn plenty of new stuff right here! Good luck for the next!
The things i have observed in terms of personal computer memory is always that there are specific features such as SDRAM, DDR or anything else, that must match the specific features of the motherboard. If the personal computer’s motherboard is kind of current while there are no computer OS issues, upgrading the ram literally requires under an hour. It’s one of the easiest pc upgrade processes one can visualize. Thanks for revealing your ideas.
I am very happy to read this. This is the kind of manual that needs to be given and not the accidental misinformation that’s at the other blogs. Appreciate your sharing this greatest doc.
It?s actually a nice and useful piece of info. I?m satisfied that you shared this useful information with us. Please keep us up to date like this. Thanks for sharing.
you’ve got a fantastic weblog here! would you prefer to make some invite posts on my blog?
I’ve been surfing on-line more than 3 hours today, yet I never discovered any interesting article like yours. It?s pretty worth enough for me. In my view, if all webmasters and bloggers made good content as you probably did, the net will be much more useful than ever before.
This design is wicked! You most certainly know how to keep a reader entertained. Between your wit and your videos, I was almost moved to start my own blog (well, almost…HaHa!) Great job. I really enjoyed what you had to say, and more than that, how you presented it. Too cool!
It?s onerous to seek out knowledgeable people on this matter, however you sound like you know what you?re speaking about! Thanks
I would like to thank you for the efforts you’ve put in writing this site. I’m hoping the same high-grade site post from you in the upcoming also. In fact your creative writing abilities has encouraged me to get my own site now. Actually the blogging is spreading its wings rapidly. Your write up is a good example of it.
I was just searching for this info for some time. After six hours of continuous Googleing, finally I got it in your site. I wonder what’s the lack of Google strategy that do not rank this kind of informative web sites in top of the list. Generally the top web sites are full of garbage.
Hello there, just became aware of your blog through Google, and found that it’s really informative. I am going to watch out for brussels. I will appreciate if you continue this in future. Many people will be benefited from your writing. Cheers!
I like what you guys are up too. Such clever work and reporting! Carry on the excellent works guys I?ve incorporated you guys to my blogroll. I think it’ll improve the value of my site 🙂
I’m not sure exactly why but this web site is loading very slow for me. Is anyone else having this problem or is it a problem on my end? I’ll check back later on and see if the problem still exists.
It is the best time to make a few plans for the long run and it is time to be happy. I have read this submit and if I may just I wish to recommend you some interesting things or suggestions. Perhaps you could write subsequent articles regarding this article. I wish to learn more things about it!
Thank you sharing most of these wonderful discussions. In addition, the best travel and also medical insurance strategy can often eliminate those fears that come with touring abroad. The medical emergency can shortly become very costly and that’s sure to quickly place a financial burden on the family’s finances. Setting up in place the perfect travel insurance offer prior to setting off is definitely worth the time and effort. Thanks
Throughout this great scheme of things you secure a B+ for effort and hard work. Exactly where you confused everybody was first in the details. As it is said, details make or break the argument.. And it could not be more accurate in this article. Having said that, allow me reveal to you just what did give good results. The authoring is really powerful and this is possibly the reason why I am taking an effort in order to opine. I do not make it a regular habit of doing that. Next, while I can certainly see a jumps in logic you come up with, I am not necessarily confident of how you appear to connect your ideas which in turn make your final result. For the moment I will, no doubt subscribe to your issue but trust in the future you actually connect the facts better.
My brother suggested I might like this website. He was entirely right. This submit truly made my day. You cann’t believe simply how much time I had spent for this info! Thanks!
We are a group of volunteers and starting a new scheme in our community. Your site offered us with valuable information to work on. You’ve done a formidable job and our entire community will be grateful to you.
Aw, this was a really nice post. In thought I wish to put in writing like this additionally ? taking time and actual effort to make an excellent article? however what can I say? I procrastinate alot and in no way appear to get one thing done.
Hello There. I discovered your weblog the usage of msn. That is an extremely neatly written article. I?ll be sure to bookmark it and return to learn extra of your helpful info. Thanks for the post. I will definitely return.
Thanks for this wonderful article. One other thing is that nearly all digital cameras arrive equipped with some sort of zoom lens so that more or less of your scene to become included by simply ‘zooming’ in and out. These kind of changes in {focus|focusing|concentration|target|the a**** length are reflected from the viewfinder and on substantial display screen right at the back of the actual camera.
This was beautiful Admin. Thank you for your reflections.
Howdy! I know this is somewhat off topic but I was wondering which blog platform are you using for this site? I’m getting fed up of WordPress because I’ve had issues with hackers and I’m looking at alternatives for another platform. I would be awesome if you could point me in the direction of a good platform.
I learned more something totally new on this losing weight issue. One particular issue is a good nutrition is tremendously vital whenever dieting. A huge reduction in bad foods, sugary meals, fried foods, sugary foods, red meat, and white-colored flour products can be necessary. Having wastes bloodsuckers, and poisons may prevent goals for fat-loss. While certain drugs for the short term solve the situation, the horrible side effects will not be worth it, they usually never offer you more than a short lived solution. It can be a known idea that 95 of fad diets fail. Thank you for sharing your notions on this website.
Nice post. I was checking continuously this blog and I am impressed! Very helpful information specially the last part 🙂 I care for such information a lot. I was seeking this certain information for a long time. Thank you and best of luck.
Thanks for the helpful write-up. It is also my opinion that mesothelioma cancer has an very long latency time, which means that signs of the disease might not exactly emerge until eventually 30 to 50 years after the first exposure to asbestos. Pleural mesothelioma, which is the most common type and has effects on the area within the lungs, will cause shortness of breath, torso pains, including a persistent coughing, which may result in coughing up bloodstream.
It’s my belief that mesothelioma will be the most dangerous cancer. It contains unusual features. The more I look at it the greater I am certain it does not respond like a true solid flesh cancer. If perhaps mesothelioma is a rogue virus-like infection, in that case there is the prospects for developing a vaccine and also offering vaccination for asbestos open people who are open to high risk regarding developing upcoming asbestos linked malignancies. Thanks for expressing your ideas on this important ailment.
Good day! Would you mind if I share your blog with my myspace group? There’s a lot of folks that I think would really enjoy your content. Please let me know. Thank you
Howdy would you mind sharing which blog platform you’re using? I’m planning to start my own blog in the near future but I’m having a tough time deciding between BlogEngine/Wordpress/B2evolution and Drupal. The reason I ask is because your design and style seems different then most blogs and I’m looking for something completely unique. P.S Apologies for being off-topic but I had to ask!
I am really impressed with your writing skills and also with the layout on your blog. Is this a paid theme or did you modify it yourself? Either way keep up the nice quality writing, it?s rare to see a nice blog like this one today..
Hello, Neat post. There’s a problem with your website in web explorer, would check this? IE nonetheless is the market leader and a big component of folks will pass over your great writing due to this problem.
I’m not that much of a internet reader to be honest but your blogs really nice, keep it up! I’ll go ahead and bookmark your site to come back down the road. Many thanks
I additionally believe that mesothelioma is a exceptional form of most cancers that is normally found in all those previously subjected to asbestos. Cancerous tissue form while in the mesothelium, which is a protective lining that covers almost all of the body’s internal organs. These cells normally form inside the lining on the lungs, tummy, or the sac which encircles the heart. Thanks for discussing your ideas.
Thanks for your text. I would also like to say that a health insurance brokerage also works for the benefit of the coordinators of the group insurance cover. The health agent is given an index of benefits needed by individuals or a group coordinator. Such a broker may is try to find individuals or perhaps coordinators that best match those demands. Then he reveals his suggestions and if the two of you agree, this broker formulates an agreement between the 2 parties.
I believe that avoiding ready-made foods is a first step in order to lose weight. They will taste beneficial, but packaged foods include very little vitamins and minerals, making you try to eat more to have enough power to get over the day. Should you be constantly consuming these foods, transitioning to grain and other complex carbohydrates will help you have more vigor while having less. Interesting blog post.
Hello there, You’ve done a fantastic job. I?ll certainly digg it and personally recommend to my friends. I’m sure they’ll be benefited from this website.
As I website possessor I believe the content material here is rattling fantastic , appreciate it for your hard work. You should keep it up forever! Best of luck.
I like what you guys are up too. This kind of clever work and coverage! Keep up the wonderful works guys I’ve included you guys to my blogroll.
I have been browsing online more than 3 hours today, yet I never found any interesting article like yours. It?s pretty worth enough for me. Personally, if all web owners and bloggers made good content as you did, the internet will be much more useful than ever before.
Hi would you mind stating which blog platform you’re using? I’m going to start my own blog in the near future but I’m having a difficult time deciding between BlogEngine/Wordpress/B2evolution and Drupal. The reason I ask is because your design seems different then most blogs and I’m looking for something unique. P.S My apologies for being off-topic but I had to ask!
There may be noticeably a bundle to find out about this. I assume you made sure good points in features also.
Thanks for expressing your ideas on this blog. Additionally, a fable regarding the banking institutions intentions while talking about foreclosed is that the traditional bank will not have my installments. There is a degree of time that this bank is going to take payments from time to time. If you are as well deep within the hole, they’ll commonly call that you pay the payment entirely. However, i am not saying that they will not take any sort of installments at all. In case you and the bank can be capable to work one thing out, this foreclosure procedure may halt. However, in the event you continue to miss out on payments in the new strategy, the property foreclosures process can just pick up exactly where it was left off.
Write more, thats all I have to say. Literally, it seems as though you relied on the video to make your point. You definitely know what youre talking about, why throw away your intelligence on just posting videos to your blog when you could be giving us something informative to read?
I loved as much as you’ll receive carried out right here. The sketch is tasteful, your authored material stylish. nonetheless, you command get got an nervousness over that you wish be delivering the following. unwell unquestionably come further formerly again since exactly the same nearly very often inside case you shield this increase.
Heya i?m for the primary time here. I came across this board and I in finding It really useful & it helped me out much. I’m hoping to offer something back and aid others like you aided me.
Hello, I think your website could possibly be having web browser compatibility problems. When I look at your website in Safari, it looks fine however, if opening in Internet Explorer, it has some overlapping issues. I simply wanted to give you a quick heads up! Other than that, great blog.
Woah! I’m really loving the template/theme of this site. It’s simple, yet effective. A lot of times it’s difficult to get that “perfect balance” between usability and visual appeal. I must say you’ve done a amazing job with this. In addition, the blog loads extremely fast for me on Opera. Outstanding Blog!
Thanks for your posting. My partner and i have generally observed that most people are wanting to lose weight because they wish to look slim plus attractive. Nonetheless, they do not generally realize that there are additional benefits for you to losing weight additionally. Doctors insist that obese people suffer from a variety of ailments that can be directly attributed to the excess weight. Thankfully that people who definitely are overweight and suffering from numerous diseases can help to eliminate the severity of their own illnesses by simply losing weight. You possibly can see a steady but identifiable improvement in health while even a minor amount of weight loss is attained.
Thank you for another informative blog. Where else could I get that kind of information written in such an ideal way? I’ve a project that I am just now working on, and I’ve been on the look out for such info.
very good publish, i actually love this web site, carry on it
Wow that was odd. I just wrote an incredibly long comment but after I clicked submit my comment didn’t appear. Grrrr… well I’m not writing all that over again. Regardless, just wanted to say excellent blog!
whoah this weblog is great i like reading your posts. Stay up the great paintings! You realize, many individuals are hunting round for this information, you can help them greatly.
I needed to thank you for this fantastic read!! I absolutely loved every little bit of it. I have got you saved as a favorite to look at new stuff you post…
Good day! I simply would like to give a huge thumbs up for the good information you could have here on this post. I will be coming back to your blog for extra soon.
Thanks for the thoughts you have discussed here. On top of that, I believe there are several factors that will keep your car insurance policy premium straight down. One is, to think about buying cars that are within the good set of car insurance companies. Cars that happen to be expensive are more at risk of being lost. Aside from that insurance coverage is also in line with the value of your car, so the more costly it is, then higher the particular premium you spend.
Usually I do not learn post on blogs, however I would like to say that this write-up very forced me to check out and do so! Your writing taste has been amazed me. Thank you, quite great post.
Can I simply say what a relief to uncover someone that really knows what they are discussing online. You certainly understand how to bring a problem to light and make it important. More people really need to look at this and understand this side of your story. I was surprised you are not more popular since you certainly have the gift.
Hello my friend! I want to say that this article is amazing, nice written and include approximately all vital infos. I?d like to see more posts like this.
I simply couldn’t leave your website before suggesting that I actually loved the standard info a person provide to your visitors? Is going to be back regularly to check out new posts
I’m very happy to read this. This is the type of manual that needs to be given and not the random misinformation that’s at the other blogs. Appreciate your sharing this best doc.
Thanks for the distinct tips contributed on this web site. I have noticed that many insurers offer clients generous deals if they favor to insure many cars with them. A significant variety of households include several automobiles these days, especially those with elderly teenage kids still living at home, as well as savings with policies can easily soon begin. So it pays off to look for a bargain.
You are so cool! I do not think I’ve truly read something like this before. So great to discover someone with a few genuine thoughts on this subject matter. Seriously.. thank you for starting this up. This site is one thing that is required on the web, someone with some originality.
I’m in awe of the author’s talent to make intricate concepts approachable to readers of all backgrounds. This article is a testament to his expertise and dedication to providing valuable insights. Thank you, author, for creating such an captivating and insightful piece. It has been an incredible joy to read!
You should be a part of a contest for one of the best websites on the internet. I most certainly will highly recommend this web site!
Pretty! This was a really wonderful post. Thank you for providing this information.
I would like to thank you for the efforts you’ve put in penning this site. I am hoping to check out the same high-grade blog posts by you later on as well. In truth, your creative writing abilities has encouraged me to get my own, personal blog now 😉
It’s hard to find knowledgeable people in this particular subject, however, you seem like you know what you’re talking about! Thanks
This really answered my downside, thank you!
Thanks for giving your ideas. I would also like to convey that video games have been actually evolving. Technology advances and revolutions have made it simpler to create authentic and active games. These types of entertainment games were not actually sensible when the concept was being experimented with. Just like other areas of technological innovation, video games also have had to advance through many ages. This is testimony towards the fast continuing development of video games.
May I simply just say what a comfort to find somebody who really knows what they are discussing on the web. You definitely understand how to bring an issue to light and make it important. More and more people need to read this and understand this side of the story. I was surprised you’re not more popular since you surely have the gift.
One thing I want to reply to is that weight loss program fast can be achieved by the proper diet and exercise. Your size not only affects the look, but also the entire quality of life. Self-esteem, depressive disorder, health risks, and also physical abilities are damaged in putting on weight. It is possible to just make everything right and at the same time having a gain. If this happens, a condition may be the primary cause. While too much food and never enough exercising are usually the culprit, common health concerns and widely used prescriptions can easily greatly enhance size. Thx for your post in this article.
I learned more something totally new on this weight reduction issue. One particular issue is a good nutrition is especially vital when dieting. A tremendous reduction in junk food, sugary ingredients, fried foods, sweet foods, beef, and white-colored flour products could be necessary. Retaining wastes organisms, and poisons may prevent ambitions for losing weight. While a number of drugs for the short term solve the situation, the bad side effects will not be worth it, and they never give more than a temporary solution. It can be a known idea that 95 of dietary fads fail. Thanks for sharing your ideas on this weblog.
Hey there! This is my first visit to your blog! We are a collection of volunteers and starting a new project in a community in the same niche. Your blog provided us beneficial information to work on. You have done a wonderful job!
I like reading through a post that will make men and women think. Also, many thanks for allowing for me to comment.
One other issue issue is that video games can be serious naturally with the key focus on knowing things rather than leisure. Although, there is an entertainment aspect to keep your kids engaged, each and every game is generally designed to work with a specific skill set or area, such as instructional math or technology. Thanks for your post.
Great paintings! This is the kind of info that are meant to be shared around the web. Shame on Google for no longer positioning this submit upper! Come on over and talk over with my website . Thank you =)
Hi, I do think this is an excellent blog. I stumbledupon it 😉 I am going to revisit once again since i have book-marked it. Money and freedom is the greatest way to change, may you be rich and continue to help others.
Pretty nice post. I just stumbled upon your blog and wanted to say that I’ve truly enjoyed surfing around your blog posts. After all I?ll be subscribing to your rss feed and I hope you write again very soon!
Thanks for revealing your ideas. I might also like to mention that video games have been actually evolving. Modern tools and inventions have made it simpler to create sensible and enjoyable games. These kinds of entertainment games were not actually sensible when the real concept was first being tried out. Just like other designs of technologies, video games also have had to develop via many many years. This is testimony for the fast development of video games.
You need to be a part of a contest for one of the most useful websites online. I will highly recommend this website!
Howdy! Do you know if they make any plugins to protect against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any recommendations?
It?s really a nice and useful piece of information. I?m happy that you just shared this helpful information with us. Please stay us up to date like this. Thank you for sharing.
A formidable share, I just given this onto a colleague who was doing somewhat analysis on this. And he the truth is bought me breakfast as a result of I discovered it for him.. smile. So let me reword that: Thnx for the deal with! But yeah Thnkx for spending the time to discuss this, I really feel strongly about it and love studying more on this topic. If potential, as you develop into expertise, would you mind updating your blog with more details? It’s highly helpful for me. Large thumb up for this blog put up!
尼卡西奥公司 III 作弊者
Thanks for your post. I would also like to opinion that the very first thing you will need to carry out is determine if you really need credit repair. To do that you will need to get your hands on a replica of your credit rating. That should not be difficult, because government makes it necessary that you are allowed to be issued one free of charge copy of the credit report annually. You just have to request that from the right individuals. You can either browse the website with the Federal Trade Commission or perhaps contact one of the leading credit agencies immediately.
Heya i?m for the primary time here. I found this board and I find It really useful & it helped me out much. I am hoping to give one thing again and aid others like you aided me.
I have been exploring for a bit for any high quality articles or weblog posts in this kind of area . Exploring in Yahoo I at last stumbled upon this site. Studying this info So i am satisfied to show that I have an incredibly just right uncanny feeling I discovered just what I needed. I most unquestionably will make sure to don?t disregard this website and provides it a glance on a continuing basis.
Thanks for the distinct tips discussed on this website. I have seen that many insurance companies offer buyers generous savings if they choose to insure a couple of cars with them. A significant quantity of households own several automobiles these days, particularly people with elderly teenage kids still residing at home, and the savings on policies can easily soon begin. So it pays to look for a great deal.
Thanks for this glorious article. One other thing is that a lot of digital cameras are available equipped with a zoom lens that allows more or less of the scene to be included by way of ‘zooming’ in and out. Most of these changes in {focus|focusing|concentration|target|the a**** length will be reflected inside the viewfinder and on big display screen on the back of the exact camera.
Kudos to the writer for providing such a comprehensive piece. Thank you for sharing your expertise!
Attractive part of content. I just stumbled upon your blog and in accession capital to assert that I acquire in fact enjoyed account your weblog posts. Any way I will be subscribing on your augment and even I fulfillment you get right of entry to constantly quickly.
Definitely believe that which you stated. Your favorite justification appeared to be on the internet the easiest thing to be aware of. I say to you, I definitely get annoyed while people consider worries that they plainly don’t know about. You managed to hit the nail upon the top and also defined out the whole thing without having side-effects , people can take a signal. Will likely be back to get more. Thanks
I think that is among the such a lot significant information for me. And i’m satisfied reading your article. But want to observation on some general things, The site style is wonderful, the articles is in reality great : D. Just right job, cheers
Hey! This post could not be written any better! Reading through this post reminds me of my good old room mate! He always kept talking about this. I will forward this write-up to him. Pretty sure he will have a good read. Many thanks for sharing!
Greetings! Quick question that’s totally off topic. Do you know how to make your site mobile friendly? My web site looks weird when browsing from my apple iphone. I’m trying to find a template or plugin that might be able to correct this problem. If you have any recommendations, please share. Thanks!
Your post has given me a fresh perspective. Thank you!
Wow! This blog looks just like my old one! It’s on a completely different topic but it has pretty much the same page layout and design. Great choice of colors!
This website definitely has all the information and facts I needed about this subject and didn’t know who to ask.
Hello there, I found your site by way of Google while searching for a comparable subject, your web site came up, it appears to be like great. I’ve bookmarked it in my google bookmarks.
I additionally believe that mesothelioma is a exceptional form of most cancers that is usually found in all those previously familiar with asbestos. Cancerous cellular material form in the mesothelium, which is a protecting lining which covers the vast majority of body’s organs. These cells ordinarily form inside the lining of your lungs, mid-section, or the sac that really encircles one’s heart. Thanks for sharing your ideas.
I have been surfing online more than 3 hours today, yet I never found any interesting article like yours. It?s pretty worth enough for me. In my opinion, if all webmasters and bloggers made good content as you did, the net will be a lot more useful than ever before.
Thanks for the suggestions shared using your blog. One more thing I would like to express is that fat reduction is not about going on a dietary fads and trying to reduce as much weight as possible in a set period of time. The most effective way to burn fat is by using it gradually and following some basic ideas which can provide help to make the most from your attempt to lose weight. You may understand and already be following a few of these tips, yet reinforcing know-how never hurts.
What i don’t realize is actually how you’re not really much more well-liked than you may be right now. You are so intelligent. You realize therefore considerably relating to this subject, made me personally consider it from a lot of varied angles. Its like women and men aren’t fascinated unless it?s one thing to do with Lady gaga! Your own stuffs outstanding. Always maintain it up!
Wonderful web site. A lot of useful information here. I?m sending it to several friends ans also sharing in delicious. And obviously, thanks for your effort!
Thanks for the something totally new you have uncovered in your short article. One thing I’d prefer to touch upon is that FSBO human relationships are built with time. By releasing yourself to owners the first weekend their FSBO will be announced, prior to masses get started calling on Thursday, you create a good link. By sending them instruments, educational elements, free reports, and forms, you become the ally. By using a personal fascination with them as well as their circumstance, you generate a solid network that, many times, pays off when the owners decide to go with an adviser they know plus trust — preferably you.
I like the valuable information you provide in your articles. I?ll bookmark your weblog and check again here regularly. I’m quite sure I will learn lots of new stuff right here! Good luck for the next!
Do you mind if I quote a couple of your articles as long as I provide credit and sources back to your blog? My blog site is in the very same niche as yours and my visitors would really benefit from some of the information you present here. Please let me know if this alright with you. Cheers!
I truly love your blog.. Pleasant colors & theme. Did you develop this web site yourself? Please reply back as I’m looking to create my own site and want to find out where you got this from or what the theme is named. Thank you!
Hoy mas que nunca los shows con webcam son una parte importante del espectaculo
I loved as much as you’ll receive carried out right here. The sketch is tasteful, your authored subject matter stylish. nonetheless, you command get bought an shakiness over that you wish be delivering the following. unwell unquestionably come further formerly again as exactly the same nearly very often inside case you shield this increase.
You’re so interesting! I do not believe I’ve truly read anything like that before. So wonderful to discover somebody with a few original thoughts on this topic. Seriously.. thank you for starting this up. This site is something that is needed on the internet, someone with some originality.
Oh my goodness! Awesome article dude! Thank you so much, However I am having issues with your RSS. I don’t know the reason why I am unable to subscribe to it. Is there anybody having identical RSS problems? Anyone who knows the solution can you kindly respond? Thanks.
I?m impressed, I have to say. Actually not often do I encounter a blog that?s each educative and entertaining, and let me inform you, you’ve gotten hit the nail on the head. Your thought is excellent; the difficulty is something that not enough persons are talking intelligently about. I’m very joyful that I stumbled throughout this in my seek for something relating to this.
Excellent site. Plenty of useful information here. I am sending it to a few friends ans also sharing in delicious. And of course, thanks for your sweat!
I’ve been absent for a while, but now I remember why I used to love this web site. Thanks , I will try and check back more often. How frequently you update your website?
The root of your writing while sounding agreeable initially, did not really sit perfectly with me after some time. Someplace within the sentences you were able to make me a believer unfortunately just for a very short while. I however have a problem with your leaps in logic and one would do well to fill in all those breaks. If you actually can accomplish that, I will undoubtedly end up being impressed.
Greetings! Very helpful advice in this particular article! It’s the little changes that make the largest changes. Thanks for sharing!
One thing is that often one of the most widespread incentives for using your card is a cash-back and also rebate supply. Generally, you’ll get 1-5 back for various buying. Depending on the credit cards, you may get 1 again on most purchases, and 5 again on expenses made using convenience stores, gasoline stations, grocery stores and ‘member merchants’.
WONDERFUL Post.thanks for share..more wait .. ?
I have observed that clever real estate agents all over the place are Advertising and marketing. They are seeing that it’s in addition to placing a sign post in the front place. It’s really with regards to building human relationships with these vendors who sooner or later will become purchasers. So, after you give your time and efforts to helping these dealers go it alone : the “Law associated with Reciprocity” kicks in. Good blog post.
I?m not sure where you’re getting your info, but great topic. I needs to spend some time learning more or understanding more. Thanks for great information I was looking for this info for my mission.
I must thank you for the efforts you’ve put in writing this blog. I am hoping to see the same high-grade blog posts from you later on as well. In fact, your creative writing abilities has encouraged me to get my own blog now 😉