Directions (1-5): The given bar graph shows the rate of interest per year by 4 various chit companies for deposits under three different plan (A, B and C).
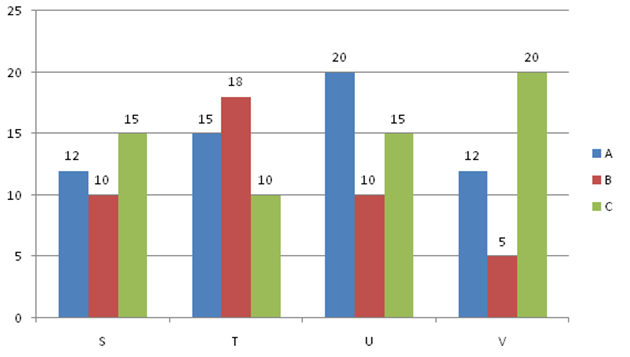
- Raj invested an amount in plan A of finance S for two years and he also invests the same amount in plan C of finance T for two years. If the total amount of simple interest accrued from the two plans is Rs.880, then what is the principal amount?
10001500200025003000Option C
x * 12 * 2/100 + x * 10 * 2/100 = 880
24x + 20x = 88000
x = Rs. 2000 - The finance U offers compound interest under plan B and finance V offer simple interest under plan B. What is the difference between the interests earned under these plans in two years, if the principal amount is Rs.8400?
543445924876456Option C
SI = 5 * 8400 * 2/100
SI = Rs. 840
CI = 8400 * (1 + 10/100)2 – 8400
CI = Rs. 1764
Required Difference = 1764 – 840 = Rs. 924 - Sam invested his amount Rs.4500 for eight years with finance T under plan B which is offering simple interest and Prem invested Rs.6000 for three years with finance V under plan C which is offering compound interest. What is the difference between the interest earned by Sam and Prem?
21122008243220022080Option A
Interest amount earned by Sam = 4500 * 18 * 8/100 = Rs. 6480
Interest amount earned by Prem = 6000 * (1 + 20/100)3 – 6000
= Rs. 4368
Required Difference = 6480 – 4368 = Rs. 2112 - Krupa invested Rs.3000 in finance S under plan C which is offering simple interest for 5 years and Rs.2000 in finance V under plan A which is also offering simple interest for 4 years, What is the total interest earned by Krupa?
30003210312032223111Option B
Total interest = 3000 * 15 * 5/100 + 2000 * 12 * 4/100
= 2250 + 960
= Rs. 3210 - The finance T offers compound interest under plan C and finance U offer simple interest under plan B. What is the difference between the interests earned under these plans in three years, if the principal amount is Rs.4800?
123134.4148.8112.7126.9Option C
Difference = P * r * r/100 * 100 * 100 * (300 + r)
= 4800 * 10 * 10/100 * 100 * 100 * (300 + 10)
= 48 * 310/100
= Rs. 148.8
If 25% of red car taken from garage A and added to garage E, then find the probability of taken two car both are pink colour in garage E105/137810/1378105/137105/37816/1378Option A
Garage A:
Let us take the no. of green colour car be x
Probability = xc1/(32+x)c1
9/25 = x/(32+x)
32*9 +9x = 25x
16x = 32*9=> x= 18 green colour car
Garage B:
Let us take the no. of green colour car be x
Probability = xc1/(34+x)c1
3/20 = x/(34+x)
3*34+ 3x = 20x
=>3*34= 17x
X= 6 green colour car
Garage C:
Let us take the no. of green colour car be x
Probability = xc1/(40+x)c1
1/5 = x/(40+x)
=>40+x= 5x
=>4x=40 =>x= 10 green colour car
Garage D:
Let us take the no. of green colour car be x
Probability = xc1/(26+x)c1
2/15 = x/(26+x)
52+2x= 15x
=>13x= 52
=> x= 4 green colour car
Garage E:
Let us take the no. of green colour car be x
Probability = xc1/(40+x)c1
1/5 = x/(40+x)
=>40+x= 5x
=>4x=40 =>x= 10 green colour car1) Answer: c)
Total number of balls in garage E = [(12*25/100)+15] +10+15+10
= 18+10+15+10
= 53
Required probability = 15c2/53c2 = (15*14)/(53*52)
= 105/1378- If the total no of red colour car and pink colour car from all the garages (A, B, C, D and E) are taken out and filled in a new garage P, then 2 car taken out from garage P find the probability of different colours
3869/78386/78753869/7875369/7875318/7875Option C
Total number of red colour cars in garage P = (12+8+10+8+15) = 53
Total number of pink colour cars in garage P = (12+16+18+12+15) = 73
Required probability = (53*73)/(53+73)c2
= 53*73/(126*125/1*2) = 3869/7875 - Four car taken from garage C, then find the probability of different colour
216/2303216/230516/2303216/303200/2303Option A
Required probability = (10*12*18*10)/50c4
= (10*12*18*10)/(50*49*48*47/1*2*3*4)
= (24*9)/(49*47)
= 216/2303 - Total number of balls in garage B and D together is approximately what percentage of the total number of balls in garage C and E together?
40%70%60%75%80%Option B
Required percentage
= [(8+10+16+6+8+6+12+4)/(10+12+18+10+15+10+15+10)]*100
= 70/100 * 100 = 70% - Two cars took randomly from garage B. What is the probability of at least one pink colour car?
42/6542/6342/6142/6739/65Option A
Required probability = 1- 24c2/40c2
= 1 – (24*23/40*39)
= 1- 23/65
= 42/65
Directions (6-10): The bar graph shows the no. of Red, Blue and Pink color cars in a garage A, B, C, D and E

Line graph shows the probability of a green color car taken from each garage.


It is in point of fact a nice and helpful piece of information. I am satisfied that you just shared this helpful info with us. Please stay us up to date like this. Thank you for sharing.
Today, with all the fast lifestyle that everyone leads, credit cards get this amazing demand throughout the economy. Persons throughout every area of life are using credit card and people who are not using the credit cards have arranged to apply for even one. Thanks for giving your ideas on credit cards.
We are a group of volunteers and opening a new scheme in our community. Your site offered us with useful information to paintings on. You have performed an impressive activity and our whole neighborhood might be grateful to you.
We are a bunch of volunteers and starting a brand new scheme in our community. Your website offered us with useful info to work on. You have done a formidable activity and our whole neighborhood will probably be thankful to you.
One other thing I would like to mention is that rather than trying to accommodate all your online degree training on days that you end work (because most people are tired when they return home), try to have most of your classes on the weekends and only a couple of courses for weekdays, even if it means taking some time away from your saturday and sunday. This is really good because on the weekends, you will be extra rested plus concentrated with school work. Thanks a lot for the different points I have mastered from your blog site.
One other thing I would like to express is that instead of trying to suit all your online degree lessons on times that you end work (considering that people are exhausted when they go back home), try to obtain most of your lessons on the weekends and only a few courses for weekdays, even if it means taking some time off your saturdays. This pays off because on the week-ends, you will be far more rested along with concentrated on school work. Thx for the different points I have realized from your web site.
Wow! This could be one particular of the most helpful blogs We’ve ever arrive across on this subject. Actually Magnificent. I am also a specialist in this topic so I can understand your effort.
Hey very nice blog!! Man .. Excellent .. Amazing .. I’ll bookmark your blog and take the feeds also?I am happy to find a lot of useful information here in the post, we need develop more techniques in this regard, thanks for sharing. . . . . .
Thanks for your article. It is extremely unfortunate that over the last years, the travel industry has already been able to to fight terrorism, SARS, tsunamis, influenza, swine flu, and also the first ever real global tough economy. Through everthing the industry has really proven to be effective, resilient along with dynamic, acquiring new methods to deal with difficulty. There are continually fresh challenges and the opportunity to which the market must once again adapt and behave.
I like what you guys are up also. Such intelligent work and reporting! Carry on the superb works guys I?ve incorporated you guys to my blogroll. I think it’ll improve the value of my web site 🙂
Hello there, just became alert to your blog through Google, and found that it is really informative. I?m going to watch out for brussels. I?ll be grateful if you continue this in future. Many people will be benefited from your writing. Cheers!
Hiya, I am really glad I’ve found this info. Today bloggers publish only about gossips and internet and this is really frustrating. A good site with interesting content, that is what I need. Thank you for keeping this website, I will be visiting it. Do you do newsletters? Can not find it.
I have seen many useful factors on your web page about pc’s. However, I have got the impression that laptops are still more or less not powerful sufficiently to be a option if you normally do projects that require a great deal of power, just like video editing and enhancing. But for internet surfing, microsoft word processing, and many other common computer work they are fine, provided you do not mind small screen size. Thank you sharing your opinions.
Normally I don’t read post on blogs, however I wish to say that this write-up very forced me to try and do so! Your writing style has been amazed me. Thanks, very nice article.
Good blog! I really love how it is easy on my eyes and the data are well written. I’m wondering how I could be notified when a new post has been made. I’ve subscribed to your feed which must do the trick! Have a nice day!
The unique payment platform that earns you INSTANT CASH BACK on everything you’re buying, at stores where you’re already shopping.
I just like the valuable info you provide for your articles. I?ll bookmark your blog and check once more right here frequently. I’m somewhat sure I will learn a lot of new stuff proper right here! Good luck for the next!
I do enjoy the manner in which you have presented this particular matter and it really does provide me a lot of fodder for consideration. On the other hand, because of just what I have witnessed, I simply just wish when the actual responses stack on that people today continue to be on point and don’t get started on a tirade of the news du jour. Anyway, thank you for this fantastic piece and though I can not concur with the idea in totality, I respect your perspective.
Thanks for your exciting article. One other problem is that mesothelioma cancer is generally brought on by the breathing of materials from mesothelioma, which is a very toxic material. It truly is commonly witnessed among laborers in the building industry who have long experience of asbestos. It is also caused by living in asbestos covered buildings for a long time of time, Family genes plays a huge role, and some people are more vulnerable to the risk than others.
Thanks for your post. Another thing is that being a photographer involves not only trouble in catching award-winning photographs but also hardships in establishing the best camera suited to your requirements and most especially challenges in maintaining the quality of your camera. This really is very genuine and apparent for those photographers that are into capturing the nature’s interesting scenes — the mountains, the actual forests, the actual wild or perhaps the seas. Visiting these amazing places definitely requires a digicam that can surpass the wild’s unpleasant setting.
I like the valuable information you provide for your articles. I?ll bookmark your weblog and test once more here regularly. I am fairly sure I?ll be informed plenty of new stuff proper here! Good luck for the following!
We are the Worlds Largest Cannabis Seedbank with over 100,000 marijuana seed strains in stock.
Another thing I have really noticed is the fact for many people, low credit score is the consequence of circumstances outside of their control. As an example they may be actually saddled with an illness and as a consequence they have more bills for collections. It might be due to a job loss or the inability to do the job. Sometimes divorce process can send the budget in an opposite direction. Thank you for sharing your opinions on this website.
One other thing I would like to convey is that as opposed to trying to accommodate all your online degree training on days that you end work (as most people are worn out when they return home), try to get most of your sessions on the weekends and only a couple courses in weekdays, even if it means taking some time away from your saturday and sunday. This is beneficial because on the weekends, you will be extra rested along with concentrated with school work. Thx for the different tips I have realized from your blog.
Wow, superb blog layout! How lengthy have you been running a blog for? you make blogging look easy. The whole look of your website is excellent, let alone the content material!
Hey, you used to write wonderful, but the last several posts have been kinda boring? I miss your super writings. Past several posts are just a little bit out of track! come on!
Thanks for your post. I also feel that laptop computers are getting to be more and more popular today, and now are often the only sort of computer used in a household. Simply because at the same time that they are becoming more and more inexpensive, their working power is growing to the point where these are as strong as desktop through just a few years ago.
One other thing I would like to express is that as an alternative to trying to fit all your online degree classes on days that you end work (since most people are fatigued when they return home), try to find most of your classes on the saturdays and sundays and only a couple of courses on weekdays, even if it means taking some time off your end of the week. This is beneficial because on the week-ends, you will be extra rested as well as concentrated upon school work. Many thanks for the different ideas I have acquired from your site.
It’s my belief that mesothelioma is most dangerous cancer. It has unusual characteristics. The more I look at it the more I am convinced it does not conduct itself like a real solid flesh cancer. In the event that mesothelioma can be a rogue viral infection, so there is the prospects for developing a vaccine in addition to offering vaccination for asbestos subjected people who are vulnerable to high risk of developing long term asbestos related malignancies. Thanks for expressing your ideas about this important ailment.
Thanks for your information on this blog. One particular thing I would want to say is purchasing electronics items over the Internet is nothing new. In fact, in the past decades alone, the marketplace for online electronic devices has grown significantly. Today, you will discover practically any kind of electronic gadget and devices on the Internet, from cameras along with camcorders to computer pieces and gambling consoles.
you’re really a good webmaster. The website loading speed is amazing. It seems that you’re doing any unique trick. Moreover, The contents are masterwork. you’ve done a fantastic job on this topic!
I loved as much as you’ll receive carried out right here. The sketch is attractive, your authored subject matter stylish. nonetheless, you command get bought an impatience over that you wish be delivering the following. unwell unquestionably come further formerly again as exactly the same nearly a lot often inside case you shield this hike.
Excellent beat ! I wish to apprentice whilst you amend your site, how could i subscribe for a blog site? The account aided me a acceptable deal. I had been a little bit familiar of this your broadcast provided vivid transparent idea
There are some fascinating points in time in this article however I don?t know if I see all of them center to heart. There is some validity however I’ll take maintain opinion till I look into it further. Good article , thanks and we want extra! Added to FeedBurner as well
It?s hard to search out knowledgeable people on this matter, but you sound like you recognize what you?re talking about! Thanks
Thanks for your submission. I also feel that laptop computers have become more and more popular currently, and now are usually the only sort of computer used in a household. This is due to the fact that at the same time actually becoming more and more economical, their working power is growing to the point where these are as strong as pc’s coming from just a few years back.
Today, with the fast chosen lifestyle that everyone leads, credit cards get this amazing demand throughout the market. Persons coming from every area of life are using credit card and people who not using the card have lined up to apply for one in particular. Thanks for sharing your ideas about credit cards.
Just wish to say your article is as amazing. The clarity in your put up is simply cool and i could suppose you are an expert on this subject. Fine with your permission allow me to grasp your feed to stay up to date with impending post. Thank you one million and please keep up the gratifying work.
fantastic points altogether, you simply gained a brand new reader. What would you recommend about your post that you made some days ago? Any positive?
Hello! I just would like to give a huge thumbs up for the nice information you may have here on this post. I might be coming back to your weblog for extra soon.
I’d personally also like to say that most people that find themselves with out health insurance are typically students, self-employed and those that are unemployed. More than half in the uninsured are really under the age of Thirty five. They do not experience they are wanting health insurance since they’re young and also healthy. Its income is often spent on homes, food, and entertainment. Many individuals that do work either 100 or as a hobby are not offered insurance by their work so they proceed without owing to the rising price of health insurance in the us. Thanks for the tips you discuss through this website.
Excellent web site. Plenty of useful info here. I?m sending it to some friends ans additionally sharing in delicious. And of course, thanks on your sweat!
Good write-up, I am normal visitor of one?s web site, maintain up the excellent operate, and It’s going to be a regular visitor for a long time.
An additional issue is that video games are generally serious naturally with the main focus on understanding rather than entertainment. Although, it has an entertainment element to keep your young ones engaged, each and every game is often designed to work with a specific expertise or program, such as mathematics or research. Thanks for your article.
One other issue is that if you are in a circumstances where you do not have a co-signer then you may genuinely wish to try to wear out all of your educational funding options. You will discover many funds and other scholarship grants that will supply you with money to support with college expenses. Thanks a lot for the post.
you are really a good webmaster. The site loading speed is incredible. It seems that you are doing any unique trick. In addition, The contents are masterpiece. you’ve done a great job on this topic!
Thank you for the sensible critique. Me and my neighbor were just preparing to do a little research on this. We got a grab a book from our area library but I think I learned more from this post. I’m very glad to see such wonderful info being shared freely out there.
Thanks for sharing excellent informations. Your web-site is so cool. I am impressed by the details that you?ve on this web site. It reveals how nicely you understand this subject. Bookmarked this website page, will come back for more articles. You, my pal, ROCK! I found simply the info I already searched all over the place and just couldn’t come across. What an ideal website.
Thank you for taking the time to write such a well-researched and informative article. It’s clear that you have put a lot of effort into crafting a high-quality piece.
Hi my family member! I want to say that this article is awesome, nice written and include approximately all vital infos. I would like to see extra posts like this .
One thing I would like to say is the fact that car insurance canceling is a feared experience and if you’re doing the best things being a driver you simply will not get one. A lot of people do obtain notice that they’ve been officially dumped by their insurance company they then have to struggle to get further insurance following a cancellation. Cheap auto insurance rates usually are hard to get after a cancellation. Understanding the main reasons with regard to auto insurance cancellation can help drivers prevent completely losing in one of the most significant privileges available. Thanks for the tips shared by your blog.
Thanks for the concepts you share through this site. In addition, lots of young women that become pregnant will not even aim to get medical insurance because they worry they wouldn’t qualify. Although some states today require that insurers produce coverage regardless of pre-existing conditions. Rates on these guaranteed options are usually bigger, but when considering the high cost of health care it may be some sort of a safer strategy to use to protect your own financial potential.
The buying process at amcauto.co was fast and easy. I was able to get behind the wheel of my new truck in no time!
Thanks for your posting. I also believe that laptop computers have gotten more and more popular currently, and now will often be the only form of computer employed in a household. This is due to the fact that at the same time they are becoming more and more reasonably priced, their working power keeps growing to the point where they can be as robust as desktop computers coming from just a few years back.
Your expertise is evident in your writing, and it’s a shame that other experts in this field haven’t taken notice yet. Keep up the good work, you already have a strong readership base.
I am now not certain where you are getting your information, however good topic. I must spend a while finding out much more or understanding more. Thank you for fantastic information I used to be on the lookout for this info for my mission.
In line with my study, after a foreclosed home is available at an auction, it is common for your borrower to be able to still have the remaining unpaid debt on the mortgage loan. There are many loan providers who seek to have all rates and liens cleared by the up coming buyer. Nonetheless, depending on particular programs, regulations, and state laws and regulations there may be several loans that aren’t easily settled through the shift of lending products. Therefore, the obligation still rests on the lender that has acquired his or her property in foreclosure. Thanks for sharing your thinking on this blog site.
Thanks , I have just been searching for information about this topic for ages and yours is the greatest I have discovered till now. But, what about the bottom line? Are you sure about the source?
I?ve recently started a web site, the information you offer on this website has helped me greatly. Thank you for all of your time & work.
One important thing is that when you’re searching for a student loan you may find that you’ll want a cosigner. There are many scenarios where this is correct because you might find that you do not possess a past credit standing so the bank will require that you have someone cosign the money for you. Great post.
I believe that avoiding ready-made foods would be the first step to be able to lose weight. They will taste beneficial, but processed foods include very little nutritional value, making you feed on more only to have enough electricity to get over the day. In case you are constantly having these foods, transferring to grain and other complex carbohydrates will help you have more vitality while having less. Great blog post.
Youre so cool! I dont suppose Ive learn anything like this before. So good to seek out any individual with some original ideas on this subject. realy thanks for starting this up. this web site is one thing that is wanted on the net, somebody with a bit of originality. helpful job for bringing something new to the web!
Hello are using WordPress for your site platform? I’m new to the blog world but I’m trying to get started and set up my own. Do you need any coding expertise to make your own blog? Any help would be really appreciated!
I truly appreciate your technique of writing a blog. I added it to my bookmark site list and will
Hi there to all, for the reason that I am genuinely keen of reading this website’s post to be updated on a regular basis. It carries pleasant stuff.
For the reason that the admin of this site is working, no uncertainty very quickly it will be renowned, due to its quality contents.
Awesome! Its genuinely remarkable post, I have got much clear idea regarding from this post
great publish, very informative. I ponder why the other specialists of this sector do not notice this. You must proceed your writing. I’m sure, you have a great readers’ base already!
Good post. I study one thing more difficult on completely different blogs everyday. It will at all times be stimulating to learn content from different writers and apply a bit of one thing from their store. I?d favor to make use of some with the content material on my weblog whether or not you don?t mind. Natually I?ll provide you with a hyperlink in your web blog. Thanks for sharing.
I really like your wp web template, exactly where do you down load it through?
Thanks for the article. My partner and i have constantly observed that most people are desirous to lose weight as they wish to appear slim as well as attractive. Even so, they do not often realize that there are more benefits just for losing weight also. Doctors claim that obese people come across a variety of conditions that can be instantly attributed to their particular excess weight. Fortunately that people who definitely are overweight and also suffering from several diseases can help to eliminate the severity of their illnesses by losing weight. It’s possible to see a continuous but noticeable improvement with health as soon as even a slight amount of weight-loss is achieved.
Hey! This post could not be written any better! Reading this post reminds me of my old room mate! He always kept chatting about this. I will forward this article to him. Fairly certain he will have a good read. Thanks for sharing!
Its such as you read my mind! You seem to grasp so much about this, such as you wrote the e book in it or something. I feel that you just can do with a few p.c. to drive the message home a little bit, however other than that, that is excellent blog. A great read. I’ll definitely be back.
Thanks for the points you have discussed here. Another thing I would like to mention is that computer system memory requirements generally increase along with other innovations in the know-how. For instance, as soon as new generations of processor chips are made in the market, there’s usually a similar increase in the scale preferences of both laptop memory plus hard drive space. This is because the software program operated simply by these processor chips will inevitably rise in power to use the new technologies.
A person essentially help to make seriously posts I would state. This is the very first time I frequented your website page and thus far? I surprised with the research you made to create this particular publish incredible. Great job!
What?s Happening i’m new to this, I stumbled upon this I have found It positively useful and it has helped me out loads. I hope to contribute & aid other users like its helped me. Great job.
Magnificent beat ! I would like to apprentice while you amend your site, how could i subscribe for a blog web site? The account aided me a acceptable deal. I had been a little bit acquainted of this your broadcast provided bright clear idea
I’m really enjoying the theme/design of your website. Do you ever run into any internet browser compatibility problems? A small number of my blog readers have complained about my site not operating correctly in Explorer but looks great in Safari. Do you have any tips to help fix this issue?
Hey there, You’ve done a fantastic job. I will certainly digg it and personally suggest to my friends. I am sure they’ll be benefited from this web site.
In the great pattern of things you’ll get an A with regard to hard work. Exactly where you actually lost us was on your particulars. As people say, the devil is in the details… And it couldn’t be more accurate here. Having said that, allow me reveal to you precisely what did give good results. Your authoring is certainly rather convincing and that is probably why I am taking the effort in order to opine. I do not really make it a regular habit of doing that. 2nd, even though I can certainly see a leaps in logic you make, I am not confident of how you seem to unite your details which help to make the actual final result. For now I will yield to your point however wish in the near future you actually link the facts better.
Yet another issue is that video gaming has become one of the all-time biggest forms of excitement for people spanning various ages. Kids participate in video games, and adults do, too. The particular XBox 360 is just about the favorite gaming systems for many who love to have a lot of video games available to them, along with who like to relax and play live with others all over the world. Many thanks for sharing your thinking.
One thing I would like to say is car insurance termination is a terrifying experience so if you’re doing the best things as being a driver you won’t get one. Some people do get the notice that they have been officially dropped by their particular insurance company and several have to fight to get supplemental insurance after the cancellation. Inexpensive auto insurance rates usually are hard to get following a cancellation. Understanding the main reasons concerning the auto insurance cancelling can help car owners prevent losing one of the most crucial privileges accessible. Thanks for the tips shared by means of your blog.
Great goods from you, man. I have understand your stuff previous to and you’re just too wonderful. I really like what you’ve acquired here, certainly like what you are stating and the way in which you say it. You make it enjoyable and you still care for to keep it smart. I can not wait to read much more from you. This is really a great website.
Unquestionably believe that which you stated. Your favorite justification appeared to be on the internet the simplest thing to be aware of. I say to you, I certainly get annoyed while people consider worries that they just don’t know about. You managed to hit the nail upon the top as well as defined out the whole thing without having side effect , people could take a signal. Will likely be back to get more. Thanks
Today, I went to the beach with my kids. I found a sea shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.” She placed the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear. She never wants to go back! LoL I know this is entirely off topic but I had to tell someone!
Heya i am for the first time here. I found this board and I find It truly useful & it helped me out much. I hope to give something back and aid others like you helped me.
What i don’t realize is actually how you are not really much more well-liked than you may be right now. You are very intelligent. You realize therefore significantly relating to this subject, made me personally consider it from so many varied angles. Its like men and women aren’t fascinated unless it?s one thing to accomplish with Lady gaga! Your own stuffs outstanding. Always maintain it up!
Woah! I’m really digging the template/theme of this website. It’s simple, yet effective. A lot of times it’s tough to get that “perfect balance” between user friendliness and appearance. I must say you’ve done a superb job with this. Also, the blog loads very fast for me on Internet explorer. Superb Blog!
Spot on with this write-up, I actually think this web site wants much more consideration. I?ll most likely be once more to read rather more, thanks for that info.
Please let me know if you’re looking for a article author for your blog. You have some really good posts and I feel I would be a good asset. If you ever want to take some of the load off, I’d love to write some articles for your blog in exchange for a link back to mine. Please blast me an e-mail if interested. Cheers!
Hmm it looks like your site ate my first comment (it was extremely long) so I guess I’ll just sum it up what I wrote and say, I’m thoroughly enjoying your blog. I too am an aspiring blog writer but I’m still new to the whole thing. Do you have any suggestions for first-time blog writers? I’d really appreciate it.
A powerful share, I just given this onto a colleague who was doing a little bit evaluation on this. And he in reality bought me breakfast as a result of I found it for him.. smile. So let me reword that: Thnx for the deal with! But yeah Thnkx for spending the time to discuss this, I really feel strongly about it and love reading extra on this topic. If attainable, as you change into experience, would you mind updating your blog with extra details? It’s extremely useful for me. Big thumb up for this weblog publish!
Hello, Neat post. There is a problem with your site in web explorer, could check this? IE still is the market chief and a good portion of other people will pass over your fantastic writing because of this problem.
Thanks for your beneficial post. In recent times, I have come to be able to understand that the symptoms of mesothelioma cancer are caused by the build up of fluid involving the lining in the lung and the chest cavity. The sickness may start from the chest area and spread to other parts of the body. Other symptoms of pleural mesothelioma cancer include weight-loss, severe inhaling trouble, throwing up, difficulty ingesting, and irritation of the neck and face areas. It needs to be noted that some people having the disease tend not to experience almost any serious signs or symptoms at all.
Nice blog here! Also your site loads up very fast! What web host are you using? Can I get your affiliate link to your host? I wish my website loaded up as quickly as yours lol
I have been exploring for a little for any high-quality articles or blog posts on this sort of space . Exploring in Yahoo I finally stumbled upon this web site. Reading this info So i?m satisfied to exhibit that I’ve a very good uncanny feeling I came upon exactly what I needed. I so much surely will make sure to don?t omit this website and provides it a glance on a continuing basis.
I relish, lead to I found just what I used to be having a look for. You have ended my four day long hunt! God Bless you man. Have a great day. Bye
Peroleh pengalaman bermain slot yang responsif dan lancar dengan aplikasi aplikasi injector cheat slot maxwin ini!
I like the helpful information you provide in your articles. I will bookmark your weblog and check again here frequently. I am quite sure I?ll learn a lot of new stuff right here! Good luck for the next!
Thank you for the sensible critique. Me and my neighbor were just preparing to do a little research on this. We got a grab a book from our local library but I think I learned more from this post. I’m very glad to see such great information being shared freely out there.
Does your website have a contact page? I’m having problems locating it but, I’d like to shoot you an email. I’ve got some recommendations for your blog you might be interested in hearing. Either way, great blog and I look forward to seeing it develop over time.
Great, Thank you!
Great, Thank you!
This actually answered my problem, thanks!
Hi would you mind stating which blog platform you’re using? I’m looking to start my own blog soon but I’m having a difficult time choosing between BlogEngine/Wordpress/B2evolution and Drupal. The reason I ask is because your layout seems different then most blogs and I’m looking for something unique. P.S Apologies for getting off-topic but I had to ask!
Aplikasi ini memberi saya kesempatan untuk mengisi waktu luang saya dengan menghasilkan uang tambahan. Tidak ada waktu yang terbuang percuma.
According to my observation, after a in foreclosure process home is marketed at a bidding, it is common for any borrower in order to still have any remaining balance on the financial loan. There are many loan providers who try and have all costs and liens paid by the upcoming buyer. Nonetheless, depending on certain programs, rules, and state legal guidelines there may be a few loans that are not easily solved through the shift of financial loans. Therefore, the duty still remains on the consumer that has had his or her property in foreclosure process. Thanks for sharing your opinions on this web site.
It was wonderfull content
Thanks for giving your ideas. I’d also like to mention that video games have been at any time evolving. Better technology and enhancements have assisted create genuine and fun games. Most of these entertainment video games were not that sensible when the actual concept was being experimented with. Just like other forms of technological innovation, video games also have had to progress through many many years. This is testimony towards fast growth and development of video games.
I am now not certain where you’re getting your info, but good topic. I needs to spend a while studying more or understanding more. Thanks for magnificent information I used to be looking for this information for my mission.
Thanks a lot for sharing this with all of us you actually know what you’re talking about! Bookmarked. Kindly also visit my web site =). We could have a link exchange agreement between us!
It?s hard to seek out knowledgeable individuals on this matter, however you sound like you understand what you?re speaking about! Thanks
It’s hard to find educated people in this particular subject, however, you seem like you know what you’re talking about! Thanks
Thanks for discussing your ideas on this blog. Also, a delusion regarding the banking institutions intentions when talking about foreclosure is that the loan company will not take my installments. There is a degree of time which the bank is going to take payments occasionally. If you are far too deep in the hole, they should commonly require that you pay the payment 100 . However, i am not saying that they will not take any sort of repayments at all. When you and the traditional bank can manage to work a little something out, this foreclosure method may end. However, if you ever continue to miss payments beneath new approach, the home foreclosure process can pick up from where it was left off.
I feel that is one of the so much vital information for me. And i’m happy studying your article. But wanna statement on few general things, The web site style is great, the articles is in reality excellent : D. Just right process, cheers
Hey very cool site!! Man .. Beautiful .. Amazing .. I will bookmark your website and take the feeds also?I am happy to find numerous useful information here in the post, we need work out more strategies in this regard, thanks for sharing. . . . . .
Do you mind if I quote a couple of your posts as long as I provide credit and sources back to your blog? My blog site is in the exact same niche as yours and my users would truly benefit from a lot of the information you present here. Please let me know if this okay with you. Cheers!
Wow that was unusual. I just wrote an incredibly long comment but after I clicked submit my comment didn’t appear. Grrrr… well I’m not writing all that over again. Regardless, just wanted to say superb blog!
Simply desire to say your article is as astounding. The clearness in your post is simply nice and i could assume you’re an expert on this subject. Fine with your permission let me to grab your feed to keep up to date with forthcoming post. Thanks a million and please carry on the gratifying work.
I just could not depart your website prior to suggesting that I actually enjoyed the standard information a person provide for your visitors? Is gonna be back often to check up on new posts
business for sale
Thanks for your post right here. One thing I would like to say is most professional fields consider the Bachelor’s Degree as the entry level standard for an online certification. Though Associate College diplomas are a great way to begin with, completing a person’s Bachelors opens many entrance doors to various professions, there are numerous on-line Bachelor Diploma Programs available through institutions like The University of Phoenix, Intercontinental University Online and Kaplan. Another issue is that many brick and mortar institutions offer Online variants of their qualifications but typically for a significantly higher payment than the corporations that specialize in online qualification programs.
Greetings from Florida! I’m bored to death at work so I decided to check out your site on my iphone during lunch break. I love the information you provide here and can’t wait to take a look when I get home. I’m amazed at how quick your blog loaded on my mobile .. I’m not even using WIFI, just 3G .. Anyways, great blog!
You need to be a part of a contest for one of the finest blogs on the internet. I most certainly will highly recommend this website!
magnificent issues altogether, you simply won a emblem new reader. What may you suggest about your submit that you made a few days in the past? Any sure?
I like what you guys are up also. Such clever work and reporting! Keep up the superb works guys I?ve incorporated you guys to my blogroll. I think it will improve the value of my site 🙂
This is a terrific web page, could you be interested in doing an interview regarding just how you developed it? If so e-mail me!
Howdy! Do you know if they make any plugins to protect against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
Thanks for sharing superb informations. Your site is very cool. I’m impressed by the details that you have on this blog. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for more articles. You, my friend, ROCK! I found just the information I already searched all over the place and simply couldn’t come across. What a perfect website.
I have observed that online diploma is getting common because obtaining your degree online has become a popular selection for many people. Quite a few people have not really had a possible opportunity to attend an established college or university however seek the improved earning potential and a better job that a Bachelor Degree gives you. Still others might have a diploma in one course but would choose to pursue one thing they now possess an interest in.
I have been browsing on-line greater than three hours these days, but I by no means found any interesting article like yours. It?s beautiful worth sufficient for me. Personally, if all website owners and bloggers made good content as you did, the net shall be much more useful than ever before.
This blog was… how do you say it? Relevant!! Finally I have found something that helped me. Thank you.
hi!,I like your writing so a lot! share we be in contact more approximately your article on AOL? I need an expert on this house to unravel my problem. May be that’s you! Having a look forward to see you.
My spouse and I stumbled over here different page and thought I might as well check things out. I like what I see so i am just following you. Look forward to exploring your web page again.
This is a really good tip particularly to those fresh to the blogosphere. Brief but very precise info… Many thanks for sharing this one. A must read post!
I have read several good stuff here. Definitely worth bookmarking for revisiting. I wonder how much effort you put to create such a great informative web site.
Can I simply say what a comfort to uncover a person that really understands what they are talking about on the net. You actually know how to bring an issue to light and make it important. A lot more people must look at this and understand this side of your story. I was surprised you are not more popular because you surely have the gift.
Oh my goodness! Impressive article dude! Thank you, However I am encountering problems with your RSS. I don’t understand the reason why I am unable to join it. Is there anyone else getting the same RSS problems? Anybody who knows the solution can you kindly respond? Thanks!
Today, with all the fast way of life that everyone leads, credit cards have a big demand in the economy. Persons out of every discipline are using the credit card and people who not using the credit cards have prepared to apply for just one. Thanks for spreading your ideas in credit cards.
Thanks for any other informative site. Where else could I get that kind of info written in such a perfect means? I have a mission that I am just now working on, and I’ve been at the look out for such info.
Along with the whole thing that seems to be building within this subject material, a significant percentage of points of view tend to be quite radical. Even so, I am sorry, because I can not give credence to your entire plan, all be it radical none the less. It would seem to everybody that your commentary are actually not completely justified and in reality you are generally yourself not even fully confident of your assertion. In any case I did appreciate looking at it.
Hi, I do believe this is an excellent web site. I stumbledupon it 😉 I may revisit once again since i have bookmarked it. Money and freedom is the best way to change, may you be rich and continue to guide others.
I’m curious to find out what blog system you have been using? I’m experiencing some minor security problems with my latest site and I’d like to find something more safe. Do you have any suggestions?
Another important part is that if you are a mature person, travel insurance intended for pensioners is something you should really contemplate. The more mature you are, the harder at risk you will be for having something bad happen to you while in most foreign countries. If you are not necessarily covered by several comprehensive insurance policies, you could have a few serious troubles. Thanks for revealing your suggestions on this blog.
Thanks for your article. What I want to say is that when searching for a good internet electronics store, look for a internet site with entire information on key elements such as the privacy statement, security details, payment guidelines, as well as other terms as well as policies. Usually take time to browse the help in addition to FAQ pieces to get a better idea of how the shop operates, what they can do for you, and ways in which you can make best use of the features.
Hi, Neat post. There is a problem with your website in internet explorer, would check this? IE still is the market leader and a large portion of people will miss your excellent writing because of this problem.
Hey There. I found your blog using msn. This is a very well written article. I?ll be sure to bookmark it and return to read more of your useful info. Thanks for the post. I will certainly comeback.
Thanks for your posting. Another element is that to be a photographer consists of not only problem in taking award-winning photographs but additionally hardships in establishing the best camera suited to your needs and most especially struggles in maintaining the grade of your camera. This really is very true and clear for those photography lovers that are straight into capturing the nature’s engaging scenes – the mountains, the actual forests, the wild or the seas. Visiting these amazing places unquestionably requires a dslr camera that can live up to the wild’s tough surroundings.
This is a topic that is close to my heart… Take care! Exactly where can I find the contact details for questions?
Thanks for the ideas you are revealing on this weblog. Another thing I want to say is always that getting hold of duplicates of your credit rating in order to look at accuracy of each detail could be the first action you have to undertake in credit restoration. You are looking to thoroughly clean your credit report from damaging details problems that ruin your credit score.
Thanks a lot for the helpful content. It is also my belief that mesothelioma has an particularly long latency time, which means that warning signs of the disease would possibly not emerge right up until 30 to 50 years after the first exposure to asbestos. Pleural mesothelioma, that is certainly the most common style and impacts the area around the lungs, might cause shortness of breath, chest pains, and a persistent cough, which may produce coughing up body.
I have realized some essential things through your site post. One other point I would like to state is that there are many games out there designed in particular for preschool age youngsters. They contain pattern identification, colors, pets, and styles. These usually focus on familiarization rather than memorization. This will keep little children occupied without sensing like they are studying. Thanks
The things i have seen in terms of computer memory is the fact that there are specifications such as SDRAM, DDR etc, that must fit the specific features of the mother board. If the pc’s motherboard is very current while there are no main system issues, replacing the memory space literally usually takes under an hour or so. It’s among the easiest pc upgrade types of procedures one can visualize. Thanks for sharing your ideas.
I will right away grab your rss feed as I can’t find your e-mail subscription link or newsletter service. Do you’ve any? Please let me know in order that I could subscribe. Thanks.
Wow, awesome blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your web site is wonderful, as well as the content!
Thank you for another informative web site. Where else could I get that type of info written in such an ideal way? I’ve a project that I am just now working on, and I have been on the look out for such info.
Thank you for sharing excellent informations. Your website is very cool. I am impressed by the details that you?ve on this site. It reveals how nicely you perceive this subject. Bookmarked this website page, will come back for more articles. You, my friend, ROCK! I found just the information I already searched everywhere and simply couldn’t come across. What a great web-site.
Would you be fascinated about exchanging links?
It is the best time to make a few plans for the future and it is time to be happy. I have learn this post and if I could I desire to suggest you some attention-grabbing issues or advice. Maybe you can write subsequent articles relating to this article. I wish to read even more things approximately it!
Excellent read, I just passed this onto a friend who was doing some research on that. And he actually bought me lunch because I found it for him smile Therefore let me rephrase that: Thanks for lunch!
I’m typically to running a blog and i actually recognize your content. The article has really peaks my interest. I am going to bookmark your web site and preserve checking for brand new information.
Way cool! Some extremely valid points! I appreciate you penning this post and also the rest of the site is very good.
Nice post. I was checking continuously this blog and I’m impressed! Very helpful info specially the last part 🙂 I care for such info a lot. I was looking for this particular info for a very long time. Thank you and best of luck.
hello!,I like your writing so much! share we communicate more about your post on AOL? I require a specialist on this area to solve my problem. Maybe that’s you! Looking forward to see you.
Thanks for your write-up on the vacation industry. I might also like to add that if your senior taking into account traveling, it is absolutely crucial to buy travel cover for senior citizens. When traveling, retirees are at high risk of having a health care emergency. Having the right insurance policy package for the age group can safeguard your health and provide peace of mind.
I believe that avoiding prepared foods would be the first step for you to lose weight. They can taste beneficial, but packaged foods contain very little nutritional value, making you take in more simply to have enough vitality to get with the day. If you’re constantly eating these foods, switching to grain and other complex carbohydrates will help you have more vitality while taking in less. Good blog post.
This article is a breath of fresh air! The author’s unique perspective and insightful analysis have made this a truly engrossing read. I’m thankful for the effort he has put into producing such an educational and thought-provoking piece. Thank you, author, for sharing your expertise and stimulating meaningful discussions through your brilliant writing!
This really answered my problem, thanks!
Hi there! Would you mind if I share your blog with my myspace group? There’s a lot of people that I think would really enjoy your content. Please let me know. Many thanks
尼卡西奥公司 III 作弊者
As I web-site possessor I believe the content matter here is rattling magnificent , appreciate it for your hard work. You should keep it up forever! Best of luck.
It?s really a nice and useful piece of information. I?m glad that you shared this helpful info with us. Please stay us up to date like this. Thank you for sharing.
wonderful post, very informative. I wonder why the other specialists of this sector don’t notice this. You must continue your writing. I’m confident, you have a great readers’ base already!
Can I simply say what a aid to seek out someone who truly knows what theyre talking about on the internet. You definitely know the right way to convey an issue to mild and make it important. Extra individuals have to read this and perceive this aspect of the story. I cant consider youre not more standard since you undoubtedly have the gift.
Please let me know if you’re looking for a writer for your weblog. You have some really good articles and I feel I would be a good asset. If you ever want to take some of the load off, I’d really like to write some content for your blog in exchange for a link back to mine. Please blast me an email if interested. Kudos!
Thanks for your publication. One other thing is always that individual American states have their own personal laws that affect house owners, which makes it very difficult for the our elected representatives to come up with a different set of rules concerning home foreclosure on property owners. The problem is that a state features own legislation which may work in an unwanted manner in terms of foreclosure policies.
I’m impressed, I must say. Seldom do I come across a blog that’s both educative and entertaining, and let me tell you, you’ve hit the nail on the head. The issue is something that too few men and women are speaking intelligently about. I am very happy I came across this in my hunt for something relating to this.
I?ve read several good stuff here. Definitely worth bookmarking for revisiting. I surprise how much effort you put to create such a excellent informative site.
Sweet blog! I found it while searching on Yahoo News. Do you have any tips on how to get listed in Yahoo News? I’ve been trying for a while but I never seem to get there! Many thanks
You need to participate in a contest for top-of-the-line blogs on the web. I will recommend this web site!
My brother suggested I might like this blog. He was entirely right. This post actually made my day. You cann’t imagine just how much time I had spent for this info! Thanks!
I’m not sure exactly why but this site is loading incredibly slow for me. Is anyone else having this issue or is it a issue on my end? I’ll check back later on and see if the problem still exists.
There’s noticeably a bundle to learn about this. I assume you made sure nice factors in features also.
Wonderful blog! I found it while surfing around on Yahoo News. Do you have any suggestions on how to get listed in Yahoo News? I’ve been trying for a while but I never seem to get there! Many thanks
An outstanding share! I have just forwarded this onto a co-worker who had been conducting a little research on this. And he in fact ordered me dinner simply because I found it for him… lol. So let me reword this…. Thanks for the meal!! But yeah, thanks for spending time to talk about this topic here on your web site.
Nice weblog right here! Additionally your website lots up very fast! What host are you using? Can I am getting your affiliate hyperlink for your host? I desire my web site loaded up as fast as yours lol
There is noticeably a bundle to find out about this. I assume you made certain nice points in features also.
Holy cow! I’m in awe of the author’s writing skills and talent to convey complicated concepts in a straightforward and precise manner. This article is a true gem that earns all the accolades it can get. Thank you so much, author, for providing your expertise and giving us with such a valuable treasure. I’m truly grateful!
One thing I’d like to say is that often before buying more computer system memory, have a look at the machine within which it could be installed. If the machine is running Windows XP, for instance, the particular memory threshold is 3.25GB. Setting up greater than this would merely constitute just a waste. Make certain that one’s mother board can handle the particular upgrade amount, as well. Thanks for your blog post.
I have seen that expenses for on-line degree experts tend to be a great value. For example a full Bachelor’s Degree in Communication in the University of Phoenix Online consists of Sixty credits at $515/credit or $30,900. Also American Intercontinental University Online offers a Bachelors of Business Administration with a entire study course feature of 180 units and a tuition fee of $30,560. Online studying has made having your college degree much simpler because you can certainly earn your own degree through the comfort of your house and when you finish working. Thanks for all other tips I have certainly learned from your web site.
Simply wish to say your article is as astounding. The clarity to your put up is simply nice and i can think you’re knowledgeable in this subject. Fine along with your permission allow me to seize your RSS feed to stay up to date with approaching post. Thank you 1,000,000 and please carry on the rewarding work.
I appreciate, cause I found exactly what I was looking for. You have ended my four day long hunt! God Bless you man. Have a great day. Bye
I was recommended this website through my cousin. I am now not sure whether or not this publish is written via him as nobody else recognise such special approximately my problem. You are incredible! Thanks!
I?d need to check with you here. Which isn’t something I normally do! I take pleasure in studying a post that may make people think. Additionally, thanks for allowing me to remark!
I was more than happy to find this net-site.I wanted to thanks for your time for this excellent read!! I definitely having fun with every little bit of it and I’ve you bookmarked to take a look at new stuff you blog post.
Spot on with this write-up, I really suppose this web site wants much more consideration. I?ll in all probability be once more to read way more, thanks for that info.
It?s exhausting to search out educated people on this topic, but you sound like you recognize what you?re talking about! Thanks
I have noticed that online education is getting popular because obtaining your college degree online has developed into popular alternative for many people. Numerous people have definitely not had an opportunity to attend a normal college or university yet seek the increased earning potential and a better job that a Bachelor Degree gives. Still other people might have a college degree in one field but would like to pursue one thing they now possess an interest in.
Excellent weblog right here! Also your website a lot up very fast! What host are you using? Can I am getting your affiliate link to your host? I wish my site loaded up as quickly as yours lol
We’re a group of volunteers and starting a new scheme in our community. Your website provided us with valuable info to work on. You have done an impressive job and our whole community will be grateful to you.
Do you mind if I quote a couple of your articles as long as I provide credit and sources back to your blog? My website is in the exact same area of interest as yours and my visitors would really benefit from some of the information you present here. Please let me know if this okay with you. Cheers!
Great write-up, I am normal visitor of one?s blog, maintain up the nice operate, and It’s going to be a regular visitor for a long time.
Sweet blog! I found it while browsing on Yahoo News. Do you have any tips on how to get listed in Yahoo News? I’ve been trying for a while but I never seem to get there! Thank you
I do believe all the ideas you’ve introduced to your post. They are very convincing and can definitely work. Still, the posts are very quick for novices. Could you please prolong them a little from next time? Thank you for the post.
We are a group of volunteers and opening a new scheme in our community. Your website provided us with valuable info to work on. You’ve done a formidable job and our whole community will be thankful to you.
Great post here. One thing I’d like to say is the fact most professional career fields consider the Bachelors Degree like thejust like the entry level standard for an online course. Whilst Associate Certification are a great way to start, completing your current Bachelors opens up many entrances to various jobs, there are numerous online Bachelor Diploma Programs available coming from institutions like The University of Phoenix, Intercontinental University Online and Kaplan. Another concern is that many brick and mortar institutions offer you Online variations of their qualifications but normally for a extensively higher amount of money than the companies that specialize in online higher education degree programs.
Good blog you’ve got here.. It’s hard to find good quality writing like yours nowadays. I truly appreciate people like you! Take care!!
I have noticed that credit restoration activity should be conducted with techniques. If not, chances are you’ll find yourself endangering your rank. In order to reach your goals in fixing your credit score you have to verify that from this moment in time you pay all of your monthly dues promptly in advance of their timetabled date. It really is significant given that by not necessarily accomplishing that, all other measures that you will decide to try to improve your credit positioning will not be successful. Thanks for sharing your thoughts.
I do agree with all of the ideas you’ve presented in your post. They are very convincing and will definitely work. Still, the posts are too short for newbies. Could you please extend them a bit from next time? Thanks for the post.
I’m blown away by the quality of this content! The author has clearly put a great amount of effort into investigating and structuring the information. It’s inspiring to come across an article that not only offers valuable information but also keeps the readers engaged from start to finish. Hats off to him for producing such a remarkable piece!
One thing I want to reply to is that weightloss routine fast is possible by the appropriate diet and exercise. A person’s size not merely affects the look, but also the actual quality of life. Self-esteem, depressive disorder, health risks, as well as physical abilities are disturbed in putting on weight. It is possible to make everything right and at the same time having a gain. If this happens, a problem may be the perpetrator. While a lot food and never enough body exercise are usually to blame, common medical conditions and widely used prescriptions can greatly increase size. Thx for your post in this article.
Also a thing to mention is that an online business administration training is designed for individuals to be able to efficiently proceed to bachelor degree programs. The Ninety credit certification meets the other bachelor diploma requirements and when you earn your associate of arts in BA online, you’ll have access to the most recent technologies on this field. Several reasons why students want to get their associate degree in business is because they may be interested in the field and want to get the general knowledge necessary prior to jumping into a bachelor diploma program. Thx for the tips you provide as part of your blog.
Hello! Do you use Twitter? I’d like to follow you if that would be okay. I’m undoubtedly enjoying your blog and look forward to new posts.
After examine a few of the blog posts in your website now, and I actually like your way of blogging. I bookmarked it to my bookmark web site listing and might be checking back soon. Pls try my web site as effectively and let me know what you think.
Hey there! I know this is kind of off topic but I was wondering if you knew where I could find a captcha plugin for my comment form? I’m using the same blog platform as yours and I’m having trouble finding one? Thanks a lot!
okmark your blog and check again here frequently. I’m quite certain I will learn many new stuff right here! Good luck for the next!
I’m really enjoying the design and layout of your site. It’s a very easy on the eyes which makes it much more pleasant for me to come here and visit more often. Did you hire out a designer to create your theme? Superb work!
Hi! I’ve been reading your blog for a long time now and finally got the courage to go ahead and give you a shout out from Humble Texas! Just wanted to mention keep up the excellent work!
Good day! I could have sworn I’ve been to your blog before but after looking at some of the articles I realized it’s new to me. Anyways, I’m certainly happy I stumbled upon it and I’ll be bookmarking it and checking back often!
Thanks for the new stuff you have unveiled in your short article. One thing I want to discuss is that FSBO relationships are built with time. By bringing out yourself to the owners the first saturday and sunday their FSBO is definitely announced, ahead of the masses begin calling on Wednesday, you build a good network. By mailing them methods, educational products, free accounts, and forms, you become the ally. By subtracting a personal interest in them along with their circumstances, you develop a solid link that, most of the time, pays off as soon as the owners opt with a real estate agent they know plus trust – preferably you actually.
I am not sure where you’re getting your information, but good topic. I needs to spend some time learning more or understanding more. Thanks for great information I was looking for this information for my mission.
When I originally commented I seem to have clicked on the -Notify me when new comments are added- checkbox and now every time a comment is added I receive 4 emails with the same comment. There has to be a means you can remove me from that service? Appreciate it.
I was just searching for this information for some time. After six hours of continuous Googleing, at last I got it in your site. I wonder what is the lack of Google strategy that do not rank this type of informative websites in top of the list. Usually the top websites are full of garbage.
This website is mostly a stroll-through for all of the data you wished about this and didn?t know who to ask. Glimpse right here, and also you?ll definitely uncover it.
I don?t even know the way I ended up here, however I assumed this post used to be great. I don’t realize who you are but definitely you’re going to a famous blogger for those who are not already 😉 Cheers!
I appreciate your wp design, exactly where would you down load it from?
I know this if off topic but I’m looking into starting my own blog and was wondering what all is required to get set up? I’m assuming having a blog like yours would cost a pretty penny? I’m not very web smart so I’m not 100 sure. Any suggestions or advice would be greatly appreciated. Cheers
naturally like your web-site however you need to check the spelling on several of your posts. A number of them are rife with spelling issues and I to find it very troublesome to inform the truth then again I?ll surely come back again.
I really like your blog.. very nice colors & theme. Did you design this website yourself or did you hire someone to do it for you? Plz answer back as I’m looking to design my own blog and would like to find out where u got this from. thanks a lot
尼卡西奥公司 III 作弊者
I blog often and I really thank you for your information. This article has truly peaked my interest. I am going to bookmark your blog and keep checking for new information about once a week. I opted in for your Feed as well.
Good post. I learn something more difficult on different blogs everyday. It’s going to at all times be stimulating to read content from different writers and follow a little one thing from their store. I?d favor to make use of some with the content on my blog whether you don?t mind. Natually I?ll provide you with a link in your net blog. Thanks for sharing.
尼卡西奥公司 III 作弊者