Quant Test for SBI PO 2018 Prelim Exam Set – 39

Banya

Hello Aspirants

State Bank of India (SBI) is going to conduct examination for its recruitment for the post of Probationary Officers (SBI PO 2018) for a total of 2000 vacancies.

Click here to know the details of the Examination

The examination will be held in three phases i.e. Preliminary Examination, Main Examination and Group Exercise & Interview. The Preliminary Exam is scheduled on 1st, 7th & 8th of July 2018. Details of the exam are as under:

Practice the questions so as to familiarize yourself with the pattern of questions to be asked in the exam. 

 

Directions(1-5): In the following questions, two equations numbered are given in variables x and y. You have to solve both the equations and find out the relationship between x and y.

  1. I. x2 + √5x – 10 = 0
    II. 2y2 + 9√5y + 50 = 0

    x=y or relation cannot be established.
    x>=y
    x>y
    y>x
    y>=x
    Option
    I. x2 + √5x – 10 = 0
    x2 + √5x – 10 = 0
    x2 + 2√5x – √5x – 10 = 0
    x = -2√5, √5
    II. 2y2 + 9√5y + 50 = 0
    2y2 + 9√5y + 50 = 0
    2y2 + 4√5y + 5√5y + 50 = 0
    y = -2√5, -5√5/2
    x ≥ y

     

  2. I. 3x2 + 16x + 20 = 0
    II. 3y2 – 14y – 5 = 0

    y>x
    x>y
    y>=x
    x>=y
    x=y or relation cannot be established.
    Option A
    I. 3x2 + 16x + 20 = 0
    3x2 + 16x + 20 = 0
    3x2 + 6x + 10x + 20 = 0
    x = -2, -10/3
    II. 3y2 – 14y – 5 = 0
    3y2 – 14y – 5 = 0
    3y2 – 15y + y – 5 = 0
    y = -1/3, 5
    x < y

     

  3. I. 4x2 + 19x + 21 = 0
    II. 2y2 – 25y – 27 = 0

    x>=y
    y>=x
    x>y
    y>x
    x=y or relation cannot be established.
    Option D
    I. 4x2 + 19x + 21 = 0
    4x2 + 19x + 21 = 0
    4x2 + 12x + 7x + 21 = 0
    x = -3, – 1.75
    I. 4x2 + 19x + 21 = 0
    2y2 – 25y – 27 = 0
    2y2 – 27y + 2y – 27 = 0
    y = 13.5, -1
    x < y

     

  4. I. 2x2 – 9x + 4 = 0
    II. 2y2 + 7y – 4 = 0

    y>=x
    x>=y
    x=y or relation cannot be established.
    y>x
    x>y
    Option B
    I. 2x2 – 9x + 4 = 0
    2x2 – 9x + 4 = 0
    2x2 – 8x – x + 4 = 0
    x = 4 , 1/2
    II. 2y2 + 7y – 4 = 0
    2y2 + 7y – 4 = 0
    2y2 + 8y – y – 4 = 0
    y = -4, ½
    x ≥ y

     

  5. I. 3x2 + 16x + 20 = 0
    II. 3y2 + 8y + 4 = 0

    x>y
    x=y or relation cannot be established.
    y>x
    y>=x
    x>=y
    Option D
    I. 3x2 + 16x + 20 = 0
    3x2 + 16x + 20 = 0
    3x2 + 6x + 10x + 20 = 0
    x = -10/3, -2
    II. 3y2 + 8y + 4 = 0
    3y2 + 8y + 4 = 0
    3y2 + 6y + 2y + 4 = 0
    y = -2, -2/3
    x ≤ y

     

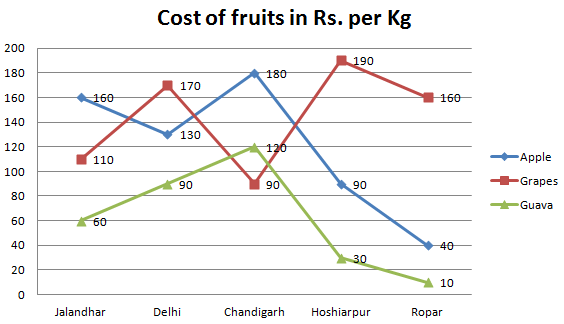
    6. Directions(6-10): Study the following graph carefully to answer the questions that follow:

  6. The cost of one kg of guava in Jalandhar is approximatelywhat per cent of the cost of two kg of grapes in Chandigarh?
    42%
    25%
    40%
    30%
    34%
    Option E
    Cost of one kg of guava in Jalandhar = 60
    Cost of two kg of grapes in Chandigarh = 90 × 2 = 180
    Required % = 60/180 × l00 =1/3 × l00
    = 33.33 = 34% (approx.)

     

  7. In which city is the difference between the cost of one kg of apple and the cost of one kg of guava the second lowest?
    Jalandhar
    Hoshiarpur
    Delhi
    Jalandhar
    Ropar
    Option C
    Cost of one kg apple in Jalandhar = 160 Cost of one kg guava in Jalandhar = 60
    Difference = 160 – 60 = 100
    Similarly, in Delhi = (130 – 90) = 40
    In Chandigarh = (180 – 120) = 60
    In Hoshiarpur = (90 – 30) = 60
    In Ropar = `(40 – 20) = 20
    Hence, the second lowest difference between price of one kg apple and one kg guava is in Delhi.

     

  8. What is the ratio of the cost of one kg of apples from Ropar to the cost of one kg of grapes from Chandigarh?
    1:3
    5:7
    2:3
    4:9
    2:5
    Option D
    Required ratio = 40/90 = 4/9

     

  9. What total amount will Ram pay to the shopkeeper for purchasing 3 kg of apples and 2 kg of guavas in Delhi?
    440
    570
    510
    405
    400
    Option B
    Total amount = 3 × 130 + 90 × 2
    = 390 + 180
    = 570

     

  10. Ravinder had to purchase 45 kg of grapes from Hoshiarpur. The shopkeeper gave him a discount of 4% per kg. What amount did he pay to the shopkeeper after the discount?
    8000
    8208
    7700
    8008
    8200
    Option B
    Cost of 45 kg grapes in Hoshiarpur = 45 × 190
    = 8550
    After 4% discount, cost price of grapes = 8550 – 8550 × 4 /100
    = 8550 – 342
    = 8208
    Hence, Ravindar had to pay 8208

     


Related posts