Directions(1-5): Find the missing term of the following series.
- 13,14,23,?,97,178
3244403648Option E
+1^2
+3^2
+5^2
+7^2
+9^2
? = 48 - 92,86,77,65,50,?
3520324150Option C
-6,-9,-12,-15,-18
? =32 - 15,17,22,31,45,?
6547605852Option A
+2,+5,+9,+14,+20
? = 65 - 8,10,?,73,297,1491
1823101427Option B
*1+2
*2+3
*3+4
*4+5
*5+6
? =23 - 7,13,25,?,67,97
3735432930Option C
+6*1
+6*2
+6*3
+6*4
+6*5
? = 43 - B and C started working together but after 8 days B is replaced by G. Now after 12 more days C is also replaced by F. For how many days F and G worked together till the work got completed?
11(4/97) days25(4/81) days20(1/93) days22(3/91) days20(4/91) daysOption E
Time taken by B,C,F and G alone to complete the work resp. = 64,52,128 and 96 days Total work = LCM (64,52,96 and 128) = 4992 units Amount of work done alone by B and C in 8 days = (78+96)*8 = 1392 days Amount of work done alone by C and G in 12 days = (96+52)*12 =1776 days Remaining work = 4992 – 1392 – 1776 = 1824 days Time taken by F and G to complete these 1824 units of work = 1824 /(39+52) = 20(4/91) days - B,F and G started working together but after 8 days F left the job and the remaining work is done by B and G together. In overall how many days does the work get completed ?
2536154022Option B
Time taken by B,F and G alone to complete the work resp. = 64 , 128 and 96 days
Total work = LCM (64,96 and 128) =384 units
Amount of work done alone by B,F and G in 8 days = (6+3+4)*8 = 104 units
Remaining work = 384 – 104 = 280 units
Time taken by B and G to complete the remaining work = 280/(6+4) = 28 days
Total time taken to complete the work = 28+ 8 = 36 days - C is 25% less efficient than X and Y is 25% more efficient than D. X and Y started working together but after 11 days Y left the job and the remaining work is done by X alone. In overall how many days the work is completed .
31(15/56) days33(19/50) days31(19/42) days31(19/56) days30(12/56) daysOption D
Time taken by C and D alone to complete the work
= 26/0.5(52 days) and 42/0.60(70 days)
Time taken by X and Y alone to complete the work = 52*0.75 (39 days) and 70/1.25 (56 days)
Total work = LCM(39 and 56) = 2184 units
Amount of work done alone by X and Y in 11 days = (56+39)*11 = 1045 units
Remaining work = 2184 – 1045 = 1139 units
Time taken by X to complete these 1139 units of work = 1139/56 = 20(19/56) days
Time taken to complete the work = 11 + 20(19/56) = 31(19/56) days - In how many days the work gets completed if A and D worked on alternate days, starting with D?
40(2/3) days44(2/9) days58(2/5) days51(3/5) days50(2/7) daysOption C
Time taken by A and D alone to complete the work resp.
= 15/0.30(50 days) and 42/0.60(70 days)
Total work = LCM(50 and 70) = 350 units
Amount of work done by A and D in two alternate days = 7+5 = 12 units
Amount of work done in 58 days = 58/2*12 = 348 units
Remaining work = 350 -348 = 2 units
Time taken by D to complete these two units of work = 2/5
Total time taken = 58(2/5) days - What is the time taken by B,C,E and F to complete the work when they are working together?
17(571/840) days10(577/807) days15(495/822) days17(577/847) days10(514/801) daysOption D
Time taken by B,C, E and F alone to complete the work resp.
= 48/0.75(64 days) , 26/0.5 (52 days), 18/0.25(72 days) and 48/0.375(128 days)
Total work = LCM (64,52,72,128) = 14976 days
Amount of work done by B,C,E and F in one day resp.
= 234 units + 288 units+ 208 units+ 117 units = 847 units
Time taken to complete the work = 14976/847
= 17(577/847) days
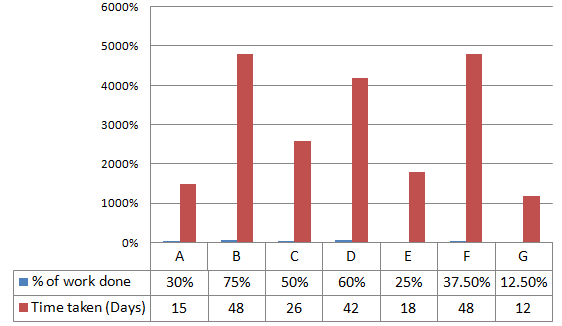
Directions(6-10): The graph given below shows the time taken by 7 people to complete the given respective percentage of the same work i.e. A alone can complete 30% of the work in 15 days.

Way cool! Some extremely valid points! I appreciate you writing this
article and the rest of the site is really good.